新疆维吾尔自治区喀什地区2024年中考数学一模模拟试题

更新时间：2024-08-17 浏览次数：25 类型：中考模拟

一、单项选择题（本大题共9小题，每小题4分，共36分，请按答题卷中的要求作答）

1. (2024·喀什模拟) 2024的倒数是（）

A . $\text{[math]}$ B . 2024 C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2024·喀什模拟) 京剧是我国的国粹，是介绍、传播中国传统艺术文化的重要媒介，在下面的四个京剧脸中，不是轴对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
3. (2024·喀什模拟) 2024年春节假期的到来，点燃了消费者的出游热情，同时也激发了旅游市场的活力.2月10日-2月17日春节假期期间，某地区累计接待游客721.76万人次，数据“721.76万”用科学记数法表示为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2024·喀什模拟) 已知一次函数 $\text{[math]}$ 的图象如图所示，则一次函数 $\text{[math]}$ 的图象大致是（）

A . B . C . D .

答案解析收藏纠错 + 选题
5. (2024·喀什模拟) 下列运算正确的是（　　）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2024·喀什模拟) 将一元二次方程 $\text{[math]}$ 通过配方转化为 $\text{[math]}$ 的形式，下列结果中正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
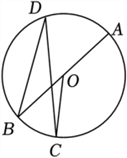
7. (2024·喀什模拟) 如图，AB是⊙O的直径，C ， D是⊙O上两点，若∠AOC＝140°，则∠BDC＝（）

A . 20° B . 40° C . 55° D . 70°

答案解析收藏纠错 + 选题
8. (2024·喀什模拟) 在 $\text{[math]}$ 中， $\text{[math]}$ ，尺规作图的痕迹如图所示．若 $\text{[math]}$ ， $\text{[math]}$ ，则线段 $\text{[math]}$ 的长为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2024·喀什模拟) 已知二次函数 $\text{[math]}$ 的图象如图所示，对称轴为直线 $\text{[math]}$ ，有下列结论：① $\text{[math]}$ ；② $\text{[math]}$ ；③ $\text{[math]}$ ；④当 $\text{[math]}$ 时， $\text{[math]}$ 随 $\text{[math]}$ 的增大而增大．其中正确的有（）

A . 4个 B . 3个 C . 2个 D . 1个

答案解析收藏纠错 + 选题

二、填空题（本大题共6小题，每小题4分，共24分．请按答题卷中的要求作答）

10. (2024·喀什模拟) 若代数式 $\text{[math]}$ 的值为0，则 $\text{[math]}$ 的值为．

答案解析收藏纠错 + 选题
11. (2024·喀什模拟) 一个正多边形的内角和是它的外角和的两倍，则这个正多边形是正边形．

答案解析收藏纠错 + 选题
12. (2024九下·上海市模拟) 有五张看上去无差别的卡片，正面分别写着 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， 0．背面朝上混合后随机抽取一张，取出的卡片正面的数字是无理数的概率是．

答案解析收藏纠错 + 选题
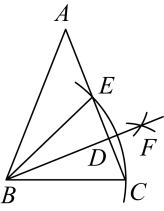
13. (2024·喀什模拟) 如图， $\text{[math]}$ 中， $\text{[math]}$ ，以点B为圆心， $\text{[math]}$ 的长为半径画弧交 $\text{[math]}$ 于点C，E，再分别以点C与点E为圆心，大于 $\text{[math]}$ 长的一半为半径画弧，两弧交于点F，连接 $\text{[math]}$ 交AC于点D，若 $\text{[math]}$ ，则 $\text{[math]}$ 是°．

答案解析收藏纠错 + 选题
14. (2024·喀什模拟) 如图，点 $\text{[math]}$ 是反比例函数 $\text{[math]}$ 图像上的一点，过 $\text{[math]}$ 作 $\text{[math]}$ 轴于点 $\text{[math]}$ ，点 $\text{[math]}$ 为 $\text{[math]}$ 轴正半轴上一点且 $\text{[math]}$ ，连接 $\text{[math]}$ 交 $\text{[math]}$ 轴于点 $\text{[math]}$ ，连接 $\text{[math]}$ ．若 $\text{[math]}$ 的面积为 $\text{[math]}$ ，则 $\text{[math]}$ 的值为．

答案解析收藏纠错 + 选题
15. (2024·喀什模拟) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ 点 $\text{[math]}$ 是线段 $\text{[math]}$ 上一动点，将 $\text{[math]}$ 沿直线 $\text{[math]}$ 折叠，使点 $\text{[math]}$ 落在点 $\text{[math]}$ 处， $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ．当 $\text{[math]}$ 是直角三角形时， $\text{[math]}$ 的长为．

答案解析收藏纠错 + 选题

三、解答题（本大题共8小题，共90分．解答应写出必要的文字说明、证明过程或演算步骤）

16. (2024·喀什模拟)
1. （1）计算： $\text{[math]}$ ．
2. （2）化简： $\text{[math]}$ ．
答案解析收藏纠错 + 选题
17. (2024·喀什模拟)
1. （1）解不等式组 $\text{[math]}$ ，并把解集在数轴上表示出来．
2. （2） 2024年是中国农历甲辰龙年．某商场用3000元购进了一批“小金龙”布偶玩具，面市后供不应求，商场又用6600元购进了第二批这种玩具，所购数量是第一批购进数量的2倍，但每件的进价贵了3元，求商场购进第一批“小金龙”每件的进价．
答案解析收藏纠错 + 选题
18. (2024·喀什模拟) 在Rt△ABC中，∠BAC＝90°，D是BC的中点，E是AD的中点，过点A作AF∥BC交BE的延长线于点F．
1. （1）求证：△AEF≌△DEB；
2. （2）证明四边形ADCF是菱形．
答案解析收藏纠错 + 选题
19. (2024·喀什模拟) 某校为落实“双减”工作，增强课后服务的吸引力，充分用好课后服务时间，为学有余力的学生拓展学习空间，成立了5个活动小组（每位学生只能参加一个活动小组）： $\text{[math]}$ ．音乐； $\text{[math]}$ ．体育； $\text{[math]}$ ．美术； $\text{[math]}$ ．阅读； $\text{[math]}$ ．人工智能．为了解学生对以上活动的参与情况，随机抽取部分学生进行了调查统计，并根据统计结果，绘制了如图所示的两幅不完整的统计图．
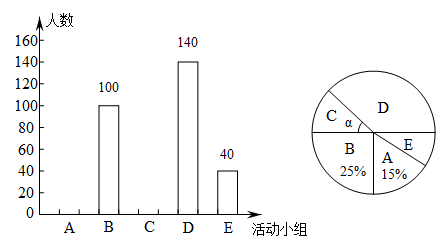
根据图中信息，解答下列问题：
1. （1） ①此次调查一共随机抽取了 ▲ 名学生；
  ②补全条形统计图（要求在条形图上方注明人数）；
  ③扇形统计图中圆心角 $\text{[math]}$ ▲ 度；
2. （2）若该校有2800名学生，估计该校参加 $\text{[math]}$ 组（阅读）的学生人数；
3. （3）学校计划从 $\text{[math]}$ 组（人工智能）的甲、乙、丙、丁四位学生中随机抽取两人参加市青少年机器人竞赛，请用树状图法或列表法求出恰好抽中甲、乙两人的概率．
答案解析收藏纠错 + 选题
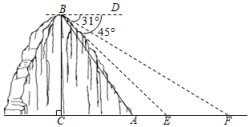
20. (2024·喀什模拟) 某镇为创建特色小镇，助力乡村振兴，决定在辖区的一条河上修建一座步行观光桥．如图，河旁有一座小山，山高 $\text{[math]}$ ，点C、A与河岸E、F在同一水平线上，从山顶B处测得河岸E和对岸F的俯角分别为 $\text{[math]}$ ， $\text{[math]}$ ．若在此处建桥，求河宽 $\text{[math]}$ 的长．（结果精确到 $\text{[math]}$ ）[参考数据： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ $\text{[math]}$

答案解析收藏纠错 + 选题
21. 某企业准备对A ， B两个生产性项目进行投资，根据其生产成本、销售情况等因素进行分析得知：投资A项目一年后的收益 $\text{[math]}$ （万元）与投入资金x（万元）的函数表达式为： $\text{[math]}$ ，投资B项目一年后的收益 $\text{[math]}$ （万元）与投入资金x（万元）的函数表达式为： $\text{[math]}$ ．
1. （1）若将10万元资金投入A项目，一年后获得的收益是多少？
2. （2）若对A ， B两个项目投入相同的资金m（ $\text{[math]}$ ）万元，一年后两者获得的收益相等，则m的值是多少？
3. （3） 2023年，我国对小微企业施行所得税优惠政策．该企业将根据此政策获得的减免税款及其他结余资金共计32万元，全部投入到A ， B两个项目中，当A ， B两个项目分别投入多少万元时，一年后获得的收益之和最大？最大值是多少万元？
答案解析收藏纠错 + 选题
22. (2024·喀什模拟) 如图，在等腰△ABC中，AB=AC，以AB为直径的⊙O与BC交于点D， DE⊥AC，垂足为E，ED的延长线与AB的延长线交于点F．
1. （1）求证：EF是⊙O的切线；
2. （2）若⊙O的半径为 $\text{[math]}$ ， BD=2，求CE的长．
答案解析收藏纠错 + 选题
23. (2024·喀什模拟) 如图，在 $\text{[math]}$ ， $\text{[math]}$ ，该三角形的三个顶点均在坐标轴上．二次函数 $\text{[math]}$ 过 $\text{[math]}$ ．
1. （1）求二次函数的解析式；
2. （2）点 $\text{[math]}$ 为该二次函数第一象限上一点，当 $\text{[math]}$ 的面积最大时，求 $\text{[math]}$ 点的坐标；
3. （3） $\text{[math]}$ 为二次函数上一点， $\text{[math]}$ 为 $\text{[math]}$ 轴上一点，当 $\text{[math]}$ 成的四边形是平行四边形时，直接写出 $\text{[math]}$ 的坐标．
答案解析收藏纠错 + 选题