重庆市荣昌中学校2023-2024学年高二下学期4月期中考试...

更新时间：2024-06-03 浏览次数：8 类型：期中考试

一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.

1. (2024高三下·长沙期中) 某学校开设5门球类运动课程、6门田径类运动课程和3门水上运动课程供学生学习，某位学生任选1门课程学习，则不同的选法共有( )

A . 90种 B . 30种 C . 14种 D . 11种

答案解析收藏纠错 + 选题
2. (2024高二下·荣昌期中) 二项式 $\text{[math]}$ 的各项系数之和为( )

A . 512 B . $\text{[math]}$ C . 2 D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2024高二下·印江月考) 若函数 $\text{[math]}$ ，则 $\text{[math]}$ （）

A . 0 B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2024高二下·荣昌期中) 从乒乓球运动员男5名、女6名中组织一场混合双打比赛，不同的组合方法种数为( )

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2024高二下·荣昌期中) 某位同学家中常备三种感冒药，分别为金花清感颗粒3盒、莲花清瘟胶囊2盒、清开灵颗粒5盒.若这三类药物能治愈感冒的概率分别为 $\text{[math]}$ ，他感冒时，随机从这几盒药物里选择一盒服用，则感冒被治愈的概率为( )

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2024高二下·荣昌期中) 已知 $\text{[math]}$ ( $\text{[math]}$ 为常数)在 $\text{[math]}$ 上有最大值3，则函数 $\text{[math]}$ 在 $\text{[math]}$ 上的最小值为( )

A . -3 B . -5 C . -37 D . -39

答案解析收藏纠错 + 选题
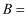
7. (2024高二下·荣昌期中) 质数(prime number)又称素数，一个大于1的自然数，除了1和它本身外，不能被其他自然数整除，则这个数为质数，数学上把相差为2的两个素数叫做“孪生素数”.如：3和5，5和 $\text{[math]}$ ，在1900年的国际数学大会上，著名数学家希尔伯特提出了23个问题，其中第8个就是大名鼎鼎的孪生素数猜想：即存在无穷多对孪生素数.我国著名数学家张益唐2013年在《数学年刊》上发表论文《素数间的有界距离》，破解了困扰数学界长达一个半世纪的难题，证明了孪生素数猜想的弱化形式.那么，如果我们在不超过30的自然数中，随机选取两个不同的数，记事件 $\text{[math]}$ “这两个数都是素数”；事件 $\text{[math]}$ “这两个数不是孪生素数”，则 $\text{[math]}$ ( )

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2024高三上·天津市期中) 已知函数 $\text{[math]}$ ，若不等式 $\text{[math]}$ 在 $\text{[math]}$ 上恒成立，则实数 $\text{[math]}$ 的取值范围是( )

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.

9. (2024高二下·荣昌期中) 已知定义域为 $\text{[math]}$ 的函数 $\text{[math]}$ 的导函数为 $\text{[math]}$ ，且 $\text{[math]}$ 的图象如图所示，则( )

A . 函数 $\text{[math]}$ 在区间 $\text{[math]}$ 上单调递增 B . 函数 $\text{[math]}$ 在 $\text{[math]}$ 上单调递减 C . 函数 $\text{[math]}$ 在 $\text{[math]}$ 处取得极小值 D . 函数 $\text{[math]}$ 在 $\text{[math]}$ 处取得极大值

答案解析收藏纠错 + 选题
10. (2024高二下·荣昌期中) 甲罐中有5个红球，5个白球，乙罐中有3个红球，7个白球.先从甲罐中随机取出一球放入乙罐，再从乙罐中随机取出一球.设 $\text{[math]}$ “从甲罐取出的球是红球”， $\text{[math]}$ “从甲罐取出的球是白球”， $\text{[math]}$ “从乙罐取出的球是红球”.则下列结论正确的是( )

A . $\text{[math]}$ 为对立事件 B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
11. (2024高二下·绵阳期末) 设函数 $\text{[math]}$ ，则( )

A . 当 $\text{[math]}$ 时，直线 $\text{[math]}$ 不是曲线 $\text{[math]}$ 的切线 B . 当 $\text{[math]}$ 时，函数 $\text{[math]}$ 有三个零点 C . 若 $\text{[math]}$ 有三个不同的零点 $\text{[math]}$ ，则 $\text{[math]}$ D . 若曲线 $\text{[math]}$ 上有且仅有四点能构成一个正方形，则 $\text{[math]}$

答案解析收藏纠错 + 选题

三、填空题:本题共3小题,每小题5分,共15分.

12. (2024高二下·益阳期中) 已知函数 $\text{[math]}$ 在点 $\text{[math]}$ 处的切线方程为 $\text{[math]}$ ，则 $\text{[math]}$ .

答案解析收藏纠错 + 选题
13. (2024高二下·荣昌期中) 若 $\text{[math]}$ ，则 $\text{[math]}$ .

答案解析收藏纠错 + 选题
14. (2024高二下·荣昌期中) 已知A ， B分别是函数 $\text{[math]}$ 和 $\text{[math]}$ 图象上的动点，若对任意的 $\text{[math]}$ ，都有 $\text{[math]}$ 恒成立，则实数 $\text{[math]}$ 的最大值为.

答案解析收藏纠错 + 选题

四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.

15. (2024高二下·荣昌期中) 已知函数 $\text{[math]}$ ，且 $\text{[math]}$ .
1. （1）求函数 $\text{[math]}$ 的图象在点 $\text{[math]}$ 处的切线方程；
2. （2）求函数 $\text{[math]}$ 的单调区间.
答案解析收藏纠错 + 选题
16. (2024高二下·荣昌期中) 在 $\text{[math]}$ 的展开式中，
1. （1）求二项式系数最大的项；
2. （2）若第 $\text{[math]}$ 项是有理项，求 $\text{[math]}$ 的取值集合.
3. （3）系数的绝对值最大的项是第几项；
答案解析收藏纠错 + 选题
17. (2024高二下·荣昌期中) 如图，在四棱锥 $\text{[math]}$ 中，四边形 $\text{[math]}$ 是正方形， $\text{[math]}$ 是等边三角形，平面 $\text{[math]}$ 平面 $\text{[math]}$ ， E，F分别是棱PC，AB的中点.
1. （1）证明： $\text{[math]}$ 平面 $\text{[math]}$ .
2. （2）求平面PBC与平面PDF夹角的余弦值.
答案解析收藏纠错 + 选题
18. (2024高二下·荣昌期中) 已知椭圆 $\text{[math]}$ 的上、下顶点分别为 $\text{[math]}$ ，点 $\text{[math]}$ 在 $\text{[math]}$ 上，且 $\text{[math]}$ .
1. （1）求椭圆 $\text{[math]}$ 的标准方程；
2. （2）设坐标原点为 $\text{[math]}$ ，若不经过点 $\text{[math]}$ 的直线与 $\text{[math]}$ 相交于 $\text{[math]}$ 两点，直线 $\text{[math]}$ 与 $\text{[math]}$ 的斜率互为相反数，当 $\text{[math]}$ 的面积最大时，求直线MN的方程.
答案解析收藏纠错 + 选题
19. (2024高二下·荣昌期中) 英国数学家泰勒发现了如下公式：
$\text{[math]}$
其中 $\text{[math]}$ 为自然对数的底数， $\text{[math]}$ .以上公式称为泰勒公式.设 $\text{[math]}$ ，根据以上信息，并结合高中所学的数学知识，解决如下问题.
1. （1）证明： $\text{[math]}$ ；
2. （2）设 $\text{[math]}$ ，证明： $\text{[math]}$ ；
3. （3）设 $\text{[math]}$ ，若 $\text{[math]}$ 是 $\text{[math]}$ 的极小值点，求实数 $\text{[math]}$ 的取值范围.
答案解析收藏纠错 + 选题