江西省南昌市二十八中教育集团联盟2024年中考数学一模试题

更新时间：2024-05-31 浏览次数：13 类型：中考模拟

一、单选题（本大题共6小题，每小题3分，共计18分）

1. (2024·桂林模拟) $\text{[math]}$ 的相反数是（）

A . $\text{[math]}$ B . 2024 C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2024·南昌模拟) 餐桌边的一蔬一饭，舌尖上的一饮一酌，实属来之不易，舌尖上的浪费让人触目惊心．据统计，中国每年浪费的食物总量折合粮食约500亿千克，这个数据用科学记数法表示为（）

A . $\text{[math]}$ 千克 B . $\text{[math]}$ 千克 C . $\text{[math]}$ 千克 D . $\text{[math]}$ 千克

答案解析收藏纠错 + 选题
3. (2024·南昌模拟) 某商场的休息椅如图所示，它的俯视图是（）

A . B . C . D .

答案解析收藏纠错 + 选题
4. (2024·南昌模拟) 下列计算正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
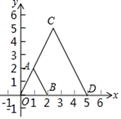
5. (2024九下·吉安期中) 如图，在平面直角坐标系xOy中，以原点O为位似中心，把线段AB放大后得到线段CD．若点A（1，2），B（2，0），D（5，0），则点A的对应点C的坐标是（）

A . (2，5) B . ( $\text{[math]}$ ，5) C . (3，5) D . (3，6)

答案解析收藏纠错 + 选题
6. (2024·南昌模拟) 如图是某男生和某女生从小学到高中身高变化情况统计图，则对于这两人的身高年增长速度的说法不正确的是（）

A . 男生在 $\text{[math]}$ 岁增长速度最快 B . 女生在 $\text{[math]}$ 岁增长速度最快 C . 男生身高年增长速度能达到 $\text{[math]}$ 厘米 $\text{[math]}$ 年 D . 女生身高年增长速度能达到 $\text{[math]}$ 厘米 $\text{[math]}$ 年

答案解析收藏纠错 + 选题

二、填空题（本大题共6小题，每小题3分，共计18分）

7. (2024·南昌模拟) 比较大小： $\text{[math]}$ 2．（填“>”或“<”）

答案解析收藏纠错 + 选题
8. (2024八下·青山湖期中) 在平面直角坐标系中，点 $\text{[math]}$ 关于原点对称的点的坐标是．

答案解析收藏纠错 + 选题
9. (2024·临川一模) 已知方程 $\text{[math]}$ 的两根分别是 $\text{[math]}$ 和 $\text{[math]}$ ，那么 $\text{[math]}$ 的值为．

答案解析收藏纠错 + 选题
10. (2024·临川一模) 如图，从一个半径为1的圆形铁皮中剪出一个圆心角为 $\text{[math]}$ 的扇形，并将剪下来的扇形围成一个圆锥，则此圆锥的底面圆的半径是．

答案解析收藏纠错 + 选题
11. (2024九下·吉安期中) 小明将两把完全相同的长方形直尺如图放置在 $\text{[math]}$ 上，两把直尺的接触点为P ，边 $\text{[math]}$ 与其中一把直尺边缘的交点为C ，点C、P在这把直尺上的刻度读数分别是2、5，则 $\text{[math]}$ 的长度是．

答案解析收藏纠错 + 选题
12. (2024·南昌模拟) 在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 是 $\text{[math]}$ 中点， $\text{[math]}$ 是 $\text{[math]}$ 上的动点，若点 $\text{[math]}$ 到 $\text{[math]}$ 的一边的距离为2，则 $\text{[math]}$ 的长为．

答案解析收藏纠错 + 选题

三、解答题（本大题共5小题，每小题6分，共计30分）

13. (2024·南昌模拟)
1. （1）计算： $\text{[math]}$
2. （2）解不等式组： $\text{[math]}$ ．
答案解析收藏纠错 + 选题
14. (2024·南昌模拟) 解方程组 $\text{[math]}$ ，下面是两同学的解答过程：
甲同学：
解：把方程 $\text{[math]}$ 变形为 $\text{[math]}$ ，再将 $\text{[math]}$ 代入方程①得 $\text{[math]}$ ， …
乙同学：
解：将方程 $\text{[math]}$ 的两边乘以3得 $\text{[math]}$ ，再将①+②，得到 $\text{[math]}$ ， …
1. （1）甲同学运用的方法是，乙同学运用的方法是；(填序号)
  ①代入消元法；②加减消元法．
2. （2）请选择一种解法，写出完整的解答过程．
答案解析收藏纠错 + 选题
15. (2024·寻乌模拟) 如图是 $\text{[math]}$ 的正方形网格，已知格点 $\text{[math]}$ （顶点在小正方形顶点处的三角形称为格点三角形），请仅用无刻度直尺完成下列作图（要求保留作图痕迹，不要求写作法）．
1. （1）图1中，在 $\text{[math]}$ 边上找一点 $\text{[math]}$ ，作线段 $\text{[math]}$ ，使得 $\text{[math]}$ ；
2. （2）图2中，在 $\text{[math]}$ 边上找一点 $\text{[math]}$ ，作线段 $\text{[math]}$ ，使得 $\text{[math]}$ ．
答案解析收藏纠错 + 选题
16. (2024九下·吉安期中) 江西省将于2024年整体实施高考综合改革．其中，考试科目将不再分文理科，改为“3+1+2”模式：“3”为全国统一考试科目语文、数学、外语；“1”为首选科目，考生从物理、历史2门科目中自主选择1门：“2”为再选科目，考生从思想政治、地理、化学、生物4门科目中自主选择2门；
1. （1）选择历史的概率是；
2. （2）请用画树状图或列表的方法，求恰好选择思想政治和地理的概率．
答案解析收藏纠错 + 选题
17. (2024·寻乌模拟) 为响应国家节能减排的倡议，某汽车专卖店销售A，B两种型号的新能源汽车，B型汽车的售价比A型汽车售价高8万元，本周售出1辆A型车和3辆B型车，销售总额为96万元．
1. （1）求每辆A型车和B型车的售价；
2. （2）随着新能源汽车越来越受消费者认可，汽车专卖店计划下周销售A，B两种型号的汽车共10辆，若销售总额不少于220万元，求B型车至少销售多少辆？
答案解析收藏纠错 + 选题

四、解答题（本大题共3小题，每小题8分，共计24分）

18. (2024·南昌模拟) 如图1是一种可折叠单面 $\text{[math]}$ 字展架，其主体部分示意图如图2，由展板 $\text{[math]}$ 、支架 $\text{[math]}$ （可绕 $\text{[math]}$ 点转动）和活动杆 $\text{[math]}$ （ $\text{[math]}$ 均为可转动支点）组成．该展架是通过改变 $\text{[math]}$ 的大小使其打开或收拢，在使用该展架时为了防止倾倒， $\text{[math]}$ 不得小于 $\text{[math]}$ ．现测得 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ．
1. （1）求支架底端 $\text{[math]}$ 张开的最大距离．
2. （2）工作人员转动支点，使 $\text{[math]}$ 与 $\text{[math]}$ 垂直后并固定（如图3），请你判断此时是否符合规范使用要求？并说明理由．（参考数据： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ）
答案解析收藏纠错 + 选题
19. (2024·南昌模拟) 为弘扬学生爱国主义教育，某校在清明节来临之际开展“走进清明·缅怀英烈”知识竞赛活动，现从七年级和八年段参加活动的学生中各随机抽取20名同学的成绩进行整理、描述和分析（成绩用x表示，共分为四组：A. $\text{[math]}$ ， B. $\text{[math]}$ ， C. $\text{[math]}$ ， D. $\text{[math]}$ ，下面给出了部分信息：
七年级学生成绩为：66，76，77，78，79，81，82，83，84，86，86，86，88，88，91，91，92，95，96，99；
八年级C组学生成绩为：88，81，84，86，87，83，89．
七、八年级学生成绩统计表：
年级
平均数
中位数
众数
方差
七年级
85.2
86
b
62.1
八年级
85.2
a
91
85.3
根据以上信息，解答下列问题：
1. （1）填空： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ；
2. （2）根据以上数据，你认为哪个年级对爱国主义教育知识掌握更好？请说明理由（写出一条理由即可）；
3. （3）该校七、八年级共840名学生参加了此次知识竞赛活动，估计两个年级成绩为优秀(90分及以上）的学生共有多少人？
答案解析收藏纠错 + 选题
20. (2024·南昌模拟) 已知：如图，已知⊙O的半径为1，菱形ABCD的三个顶点A、B、D在⊙O上，且CD与⊙O相切．
1. （1）求证：BC与⊙O相切；
2. （2）求阴影部分面积．
答案解析收藏纠错 + 选题

五、解答题（本大题共2小题，每小题9分，共计18分）

21. (2024·南昌模拟) 在实验课上，小明做了一个试验．如图，在仪器左边托盘A（固定）中放置一个物体，在右边托盘B（可左右移动）中放置一个可以装水的容器，容器的质量为5g．在容器中加入一定质量的水，可以使仪器左右平衡．改变托盘B与点C的距离 $\text{[math]}$ ，记录容器中加入的水的质量，得到下表：
托盘B与点C的距离x/cm
30
25
20
15
10
容器与水的总质量 $\text{[math]}$
10
12
15
20
30
加入的水的质量 $\text{[math]}$
5
7
10
15
25
把上表中的x与 $\text{[math]}$ 各组对应值作为点的坐标，在平面直角坐标系中描出这些点，并用光滑的曲线连接起来，得到如图所示的 $\text{[math]}$ 关于x的函数图象．
1. （1）请在该平面直角坐标系中作出 $\text{[math]}$ 关于x的函数图象；
2. （2）观察函数图象，并结合表中的数据：
  ①猜测 $\text{[math]}$ 与x之间的函数关系，并求 $\text{[math]}$ 关于x的函数表达式；
  ②求 $\text{[math]}$ 关于x的函数表达式；
  ③当 $\text{[math]}$ 时， $\text{[math]}$ 随x的增大而 ▲ (填“增大”或“减小”)， $\text{[math]}$ 随x的增大而 ▲ （填“增大”或“减小”)， $\text{[math]}$ 的图象可以由 $\text{[math]}$ 的图象向 ▲ （填“上”或“下”或“左”或“右”)平移得到．
3. （3）若在容器中加入的水的质量 $\text{[math]}$ 满足 $\text{[math]}$ ，求托盘B与点C的距离x(cm)的取值范围．
答案解析收藏纠错 + 选题
22. (2024·南昌模拟) 如图
1. （1）【问题发现】如图1，矩形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，点 $\text{[math]}$ 是矩形 $\text{[math]}$ 内一点，过点 $\text{[math]}$ 作 $\text{[math]}$ ，分别交 $\text{[math]}$ ， $\text{[math]}$ 于点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ．则：
  ① $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ；
  ② $\text{[math]}$ 与 $\text{[math]}$ 的关系是；
2. （2）【类比探究】如图2，点 $\text{[math]}$ 是矩形 $\text{[math]}$ 外一点，过点 $\text{[math]}$ 作 $\text{[math]}$ ，分别交 $\text{[math]}$ ， $\text{[math]}$ 反向延长线于点 $\text{[math]}$ ， $\text{[math]}$ ， ②中结论还成立吗？若成立，请说明理由；
3. （3）【拓展延伸】如图3，在 $\text{[math]}$ 中， $\text{[math]}$ ， P是 $\text{[math]}$ 外一点， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的最小值为．
答案解析收藏纠错 + 选题

六、解答题（本大题共1小题，每小题12分，共计12分）

23. (2024·南昌模拟) 根据以下素材，探索完成任务．

运用二次函数来研究植物幼苗叶片的生长状况
	1．在大自然里，有很多数学的奥秘．一片美丽的心形叶片、一棵生长的幼苗都可以看作把一条抛物线的一部分沿直线折叠而形成． 2．幼苗在生长过程中，叶片是越长越张开．
素材
问题解决
任务1	确定心形叶片的形状	如图3建立平面直角坐标系，心形叶片下部轮廓线可以看作是二次函数 $\text{[math]}$ 图像的一部分，且过原点，求抛物线的解析式及顶点D的坐标．
任务2	研究心形叶片的尺寸	如图3，心形叶片的对称轴直线 $\text{[math]}$ 与坐标轴交于A，B两点，抛物线与x轴交于另一点C，过点C作x轴的垂线交直线 $\text{[math]}$ 于点E，点C， $\text{[math]}$ 是叶片上的一对对称点， $\text{[math]}$ 交直线 $\text{[math]}$ 于点G．求叶片此处的宽度 $\text{[math]}$ ．
任务3	探究幼苗叶片的生长	小李同学在观察幼苗生长的过程中，发现幼苗叶片下方轮廓线都可以看作是二次函数 $\text{[math]}$ 图像的一部分．如图4，幼苗叶片下方轮廓线正好对应任务1中的二次函数．已知直线 $\text{[math]}$ （点P为叶尖）与水平线的夹角为 $\text{[math]}$ ．三天后，叶片根部D长到与点P同一水平位置的 $\text{[math]}$ 处时，叶尖Q落在射线 $\text{[math]}$ 上（如图5所示），求此时幼苗叶片的长度 $\text{[math]}$ ．