广东省佛山市顺德区德胜中学2023-2024学年七年级下学期...

更新时间：2024-06-03 浏览次数：36 类型：月考试卷

一、选择题（（本大题10小题，每小题3分，共30分）

1. (2024七下·顺德月考) 下列倡导节约的图案中，是轴对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
2. (2024七下·顺德月考) 随着北斗系统全球组网的步伐，国产北斗芯片三号信号的22nm（即0.000000022m）工艺射频基带一体化导航定位芯片已实现规模化应用，其中0.000000022用科学记数法表示为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2024七下·顺德月考) 下列计算正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2024七下·顺德月考) 刘老师到加油站加油，如图，这是他所用的加油机上某一时刻的数据显示牌，则其中的常量是（）

A . 金额 B . 单价 C . 数量 D . 金额和数量

答案解析收藏纠错 + 选题
5. (2024七下·顺德月考) 将一副直角三角板如图放置，已知 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ （）

A . 45° B . 60° C . 75° D . 105°

答案解析收藏纠错 + 选题
6. (2024七下·顺德月考) 如图，点 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 在同一直线上，若 $\text{[math]}$ $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 等于（）

A . 7 B . 8 C . 9 D . 10

答案解析收藏纠错 + 选题
7. (2024七下·顺德月考) 如图，D在AB上，E在AC上，且 $\text{[math]}$ ，补充下列一个条件仍无法判定 $\text{[math]}$ 的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2024七下·顺德月考) 小冬和小天沿同一条笔直的公路相向而行，小冬从甲地前往乙地，小天从乙地前往甲地。两人同时发出，当行驶5分钟时小冬发现重要物品忘带，立刻掉头提速返回甲地，用时4分钟，拿到物品后以提速后的速度继续前往乙地（掉头和拿物品的时间忽略不计），小天始终以一个速度保持行驶，二人相距的路程y（米）与小冬出发时间x（分钟）之间的关系如图所示，则下列说法中错误的是（）

A . 小冬返回甲地的速度与小天行驶速度相同 B . 小冬和小天出发时的速度分别为160米/分钟和200米/分钟 C . 小天出发14.5分钟两人相遇 D . 小冬最终达到乙地的时间是20分钟

答案解析收藏纠错 + 选题
9. (2024七下·顺德月考) 如图1的长方形纸带中 $\text{[math]}$ ，将纸带沿EF折叠成图2，再沿BF折叠成图3，则图3中 $\text{[math]}$ 度数是（）

A . 105° B . 120° C . 130° D . 145°

答案解析收藏纠错 + 选题
10. (2024七下·顺德月考) 小丽与爸妈在公园里荡秋千．如图，小丽坐在秋千的起始位置A处，OA与地面垂直，两脚在地面上用力一蹬，妈妈在距地面1m高的B处接住她后用力一推，爸爸在C处接住她．若妈妈与爸爸到OA的水平距离BD、CE分别为1.4m和1.8m，∠BOC＝90°．爸爸在C处接住小丽时，小丽距离地面的高度是（）．

A . 1m B . 1.6m C . 1.8m D . 1.4m

答案解析收藏纠错 + 选题

二、填空题（本大题7小题，每小题4分，共28分）

11. (2024七下·顺德月考) 计算 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
12. (2024七下·顺德月考) 利用如图所示的方法，可以折出“过已知直线外一点和已知直线平行”的直线，请说明其中的道理．

答案解析收藏纠错 + 选题
13. (2024七下·顺德月考) 声音在空气中传播的速度（声速）y（m/s）与温度x（℃）之间的关系如下：
温度/℃
0
5
10
15
20
声速/（m/s）
331
334
337
340
343
在温度为20℃的这天召开运动会，某人看到发令枪的烟0.1s后，听到了枪声，则他距离发令枪m．

答案解析收藏纠错 + 选题
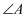
14. (2024七下·顺德月考) 一个零件的形状如图所示，按规定 $\text{[math]}$ 应等于90°， $\text{[math]}$ 与 $\text{[math]}$ 的度数分别是20°和30°，牛叔叔量得 $\text{[math]}$ ，请你帮助牛叔叔判断该零件．（填“合格”或“不合格”）

答案解析收藏纠错 + 选题
15. (2024七下·顺德月考) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ 和 $\text{[math]}$ 的平分线相交于点P ，若 $\text{[math]}$ ，则 $\text{[math]}$ 的度数为．

答案解析收藏纠错 + 选题
16. (2024七下·顺德月考) 已知∠A与∠B两边分别平行，且∠A比∠B的3倍少20°，则∠A的大小是．

答案解析收藏纠错 + 选题
17. (2024七下·顺德月考) 如图，△ABC中，∠ACB＝90°，AC＝8cm，BC＝14cm，点P从A点出发沿A→C→B路径向终点运动，终点为B点，点Q从B点出发沿B→C→A路径向终点运动，终点为A点，点P和Q分别以2cm/s和3cm/s的运动速度同时开始运动，两点都要到达相应的终点时才能停止运动，分别过P和Q作PE⊥l于E，QF⊥l于F．设运动时间为t秒，要使以点P，E，C为顶点的三角形与以点Q，F，C为顶点的三角形全等，则t的值为．

答案解析收藏纠错 + 选题

三、解答题（一）（本大题3小题，18题8分，19题、20题每小题6分，共20分）

18. (2024七下·顺德月考) 计算：
1. （1） $\text{[math]}$ ；
2. （2） $\text{[math]}$ ．
答案解析收藏纠错 + 选题
19. (2024七下·顺德月考) 如图，已知 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ．试说明： $\text{[math]}$ ．
解：∵ $\text{[math]}$ ， $\text{[math]}$ （已知），
∴ $\text{[math]}$
∴   ▲    $\text{[math]}$    ▲    ．（同位角相等，两直线平行）
∴ $\text{[math]}$ （   ▲   ）．
∵ $\text{[math]}$ （已知），
∴∠   ▲   =∠   ▲   （等量代换）．
∴ $\text{[math]}$ （   ▲   ）．

答案解析收藏纠错 + 选题
20. (2024七下·顺德月考) 如图，已知三角形ABC ．
1. （1）利用尺规，在三角形ABC的边AC上方作 $\text{[math]}$ （尺规作图要求保留作图痕迹，不写作法）
2. （2）若 $\text{[math]}$ ，直接写出AE与AB的位置关系．
答案解析收藏纠错 + 选题

四、解答题（二）（本大题2小题，每小题9分，共18分）

21. (2024七下·顺德月考) 一水果贩子在批发市场按每千克1.8元批发了若干千克的西瓜进城出售，为了方便，他带了一些零钱备用。他先按市场价售出一些后，又降价出售。售出西瓜千克数x与他手中持有的钱数y元（含备用零钱）的关系如图所示，结合图象回答下列问题：
1. （1）农民自带的零钱是多少？
2. （2）降价前他每千克西瓜出售的价格是多少？
3. （3）随后他按每千克下降0.5元将剩余的西瓜售完，这时他手中的钱（含备用的钱）是390元，问他一共批发了多少千克的西瓜？
4. （4）请问这个水果贩子一共赚了多少钱？
答案解析收藏纠错 + 选题
22. (2024七下·顺德月考) 如图， $\text{[math]}$ 中， $\text{[math]}$ ， D是BA延长线上一点，点E是∠CAD的平分线上一点，过点E作EF⊥AC于F ， EG⊥AD于G ．
1. （1）求证： $\text{[math]}$ ；
2. （2）若 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，求AF的长．
答案解析收藏纠错 + 选题

五、解答题（三）（本大题2小题，每小题12分，共24分）

23. (2024七下·顺德月考)
1. （1）【操作发现】如图1是一个长为4b、宽为a的长方形，沿图1中虚线用剪刀平均分成四块小长方形，然后用四块小长方形拼成的一个“回形”正方形（如图2），那么图2中的阴影部分的面积为：（用a ， b的代数式表示）；观察图2，请你写出 $\text{[math]}$ ， $\text{[math]}$ ， ab之间的等量关系是．
2. （2）【灵活应用】①若x ， y为有理数，且 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的值；
  ②若 $\text{[math]}$ ，求 $\text{[math]}$ 的值；
3. （3）【拓展迁移】将两块全等的特制直角三角板 $\text{[math]}$ ， $\text{[math]}$ （ $\text{[math]}$ 按如图3所示的方式放置，A ， O ， D在同一直线上，连接AC ， BD ．若 $\text{[math]}$ ， $\text{[math]}$ ，求阴影部分的面积．
答案解析收藏纠错 + 选题
24. (2024七下·顺德月考) 【问题探究】
1. （1）如图1，在四边形ABCD中，∠BAD与∠BCD互补，∠B与∠D互补， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，数学兴趣小组在探究y与x的数量关系时，经历了如下过程：
  ①数学兴趣小组通过电脑软件“几何画板”进行探究，测量出部分结果如下表所示：
  x
  …
  30
  40
  50
  60
  70
  80
  100
  θ
  …
  y
  …
  75
  70
  65
  60
  α
  50
  β
  25
  …
  这里 $\text{[math]}$ ▲ ， $\text{[math]}$ ▲ ， $\text{[math]}$ ▲ ．
  ②根据表格，猜想：y与x之间的关系式为 ▲ ；
  ③数学兴趣小组发现证明此猜想的一种方法：如图2，延长CB到E ，使 $\text{[math]}$ ，连接AE ， …，请你根据其思路将证明过程补充完整．
2. （2）如图3，D为 $\text{[math]}$ 边BC上一点， $\text{[math]}$ ，其中 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，若 $\text{[math]}$ ， $\text{[math]}$ 的面积为14，求 $\text{[math]}$ 的面积．
答案解析收藏纠错 + 选题