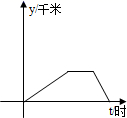
 B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 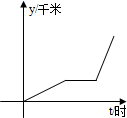


下面是小聪同学设计的尺规作图过程:
已知:如图,△ABC中,AB=AC .
求作:一点P , 使得PA=PB=PC .
作法:
①作∠BAC的平分线AM交BC于点D;
②作边AB的垂直平分线EF , EF与AM相交于点P;
③连接PB , PC .
所以,点P就是所求作的点
根据小聪同学设计的尺规作图过程,
证明:∵AB=AC , AM平分∠BAC交BC于点D ,
∴AD是BC的垂直平分线:( ▲)(填推理依据)
∴PB=PC .
∵EF垂直平分AB , 交AM于点P ,
∴PA=PB:( ▲)(填推理依据)
∴PA=PB=PC .
∵AD平分∠BAC ,
∴ ▲= ▲( ▲)(填推理的依据).


40 21 35 24 40 38 23 52 35 62 36 15 51 45 40 42 40 32 43 36 34 53 38 40 39 32 45 40 50 45 40 40 26 45 40 45 35 40 42 45

分组 | 频数 | 频率 |
14.5﹣22.5 | 2 | 0.050 |
22.5﹣30.5 | 3 | ____ |
30.5﹣38.5 | 10 | 0.250 |
38.5﹣46.5 | 19 | ____ |
46.5﹣54.5 | 5 | 0.125 |
54.5﹣62.5 | 1 | 0.025 |
合计 | 40 | 1.00 |
①如果正方形 绕点
旋转,连接
、
、
,线段
与AF的数量关系有无变化?请仅就图2的情形给出证明;
②正方形 绕点
旋转的过程中,当以点A,B,C,E为顶点的四边形是平行四边形时.直接写出线段AF的长.
