题库组卷系统-专注K12在线组卷服务

在线咨询

当前：初中数学

当前位置：初中数学 /备考专区

试卷结构：课后作业日常测验标准考试

| 显示答案解析 | 全部加入试题篮 | 平行组卷试卷细目表发布测评在线自测试卷分析收藏试卷试卷分享

下载试卷下载答题卡

广东省佛山市南海区桂城街道桂江第一初级中学2023-2024...

更新时间：2024-07-29 浏览次数：197 类型：期中考试

一、选择题：（每小题3分，共30分）

1. (2024七下·南海期中) 下列四幅图中，是轴对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
2. (2024七下·南海期中) 世卫组织宣布冠状病毒最大直径约为 $\text{[math]}$ ，“0.00000012”用科学记数法可表示为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2024七下·南海期中) 下列计算正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2024七下·南海期中) 下列每组数分别是三根小木棒的长度，用它们能摆成三角形的是（）

A . $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ B . $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ C . $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ D . $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2024七下·南海期中) 已知一个等腰三角形有一个角为80°，则顶角是（）

A . 20° B . 80° C . 20°或80° D . 不能确定

答案解析收藏纠错 + 选题
6. (2024七下·南海期中) 如图所示的网格由边长相同的小正方形组成，点A、B、C、D、E、F、G在小正方形的顶点上，则△ABC的重心是（）.

A . 点D B . 点E C . 点F D . 点G

答案解析收藏纠错 + 选题
7. (2024七下·南海期中) 已知直线m∥n，将一块含45°角的直角三角板ABC按如图方式放置，其中斜边BC与直线n交于点D.若∠1=25°，则∠2的度数为（）

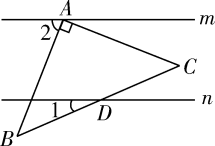
A . 60° B . 65° C . 70° D . 75°

答案解析收藏纠错 + 选题
8. (2024七下·南海期中) 如图，已知∠ABC＝∠DCB，下列结论中，不能得到△ABC≌△DCB的是（）

A . AC＝BD B . ∠A＝∠D C . AB＝CD D . ∠EBC＝∠ECB

答案解析收藏纠错 + 选题
9. (2024七下·南海期中) 如图，点E在AC的延长线上，下列条件中能判断 $\text{[math]}$ 的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2024七下·南海期中) 如图，一列快车从甲地驶往乙地，一列慢车从乙地驶往甲地，两车同时出发匀速行驶.设慢车行驶的时间为x(h)，两车之间的距离为y(km)，图中的折线表示y与x之间的函数关系．下列说法中正确的是（）

A . B点表示此时快车到达乙地 B . B-C-D段表示慢车先加速后减速最后到达甲地 C . 慢车的速度为125km/h D . 快车的速度为 $\text{[math]}$ km/h

答案解析收藏纠错 + 选题

二、填空题：（每小题3分，共15分）

11. (2024七下·南海期中) 如图，电线杆上的横梁下方用三角形的支架支撑的理论根据是.

答案解析收藏纠错 + 选题
12. (2024七下·南海期中) 已知 $\text{[math]}$ 的补角是它余角的3倍，则 $\text{[math]}$ 为.

答案解析收藏纠错 + 选题
13. (2024七下·贺兰期中) 若 $\text{[math]}$ 是一个完全平方式，则m的值是．

答案解析收藏纠错 + 选题
14. (2024七下·南海期中) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ，将其折叠，使点A落在边BC上的点E处，CA与CE重合，折痕为CD，则 $\text{[math]}$ 的度数是．

答案解析收藏纠错 + 选题
15. (2024七下·南海期中) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ 是高， $\text{[math]}$ 是中线， $\text{[math]}$ 是角平分线， $\text{[math]}$ 交 $\text{[math]}$ 于G ，交 $\text{[math]}$ 于H.下列结论：① $\text{[math]}$ ；② $\text{[math]}$ ；③ $\text{[math]}$ ；④ $\text{[math]}$ .其中所有正确结论的序号是.

答案解析收藏纠错 + 选题

三、解答题（一）：（16~20题，每小题5分，共25分）

16. (2024七下·南海期中) 计算： $\text{[math]}$

答案解析收藏纠错 + 选题
17. (2024七下·南海期中) 先化简，再求值： $\text{[math]}$ ，其中 $\text{[math]}$ ， $\text{[math]}$ .

答案解析收藏纠错 + 选题
18. (2024七下·南海期中) 如图，已知 $\text{[math]}$ ， $\text{[math]}$ .说明 $\text{[math]}$ 的理由.

答案解析收藏纠错 + 选题
19. (2024七下·南海期中) 已知：CD平分∠ACB，BF是△ABC的高，若∠A＝70°∠ABC＝60°求∠BMC的度数.

答案解析收藏纠错 + 选题
20. (2024七下·南海期中) 已知 $\text{[math]}$ 和线段b、c ，求作 $\text{[math]}$ ，使 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ .（不写作法，保留痕迹）

答案解析收藏纠错 + 选题

四、解答题（二）：（21~22题，每小题8分，23题10分，共26分）

21. (2024七下·南海期中) 已知：如图，在 $\text{[math]}$ 和 $\text{[math]}$ 中，点B ， F ， E ， D依次在一条直线上，若 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，
求证：
1. （1） $\text{[math]}$ ；
2. （2） $\text{[math]}$
答案解析收藏纠错 + 选题
22. (2024七下·南海期中) 两个大小不同的等腰直角三角板如图所示放置，右图是由它抽象出的几何图形，B ， C ， E在同一条直线上，连接DC ．
1. （1）求证：△ABE≌△ACD；
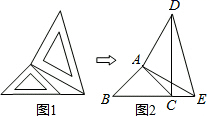
2. （2）若图2中的BE＝3CE ， CD＝6，求 △DCE的面积．
答案解析收藏纠错 + 选题
23. (2024七下·南海期中) 小明骑单车上学，当他骑了一段路时，想起要买某本书，于是又折回到刚经过的某书店，买到书后继续去学校．以下是他本次上学所用的时间与路程的关系示意图根据图中提供的信息回答下列问题：
1. （1）小明家到学校的路程是米，小明在书店停留了分钟；
2. （2）本次上学途中，小明一共行驶了米，一共用了分钟；
3. （3）在整个上学的途中（哪个时间段）小明骑车速度最快，最快的速度是米/分；
4. （4）小明出发多长时间离家1200米？
答案解析收藏纠错 + 选题

五、解答题（三）：（24~25题，每小题12分，共24分）

24. (2024七下·南海期中) 数形结合是一种重要的数学思想方法.数学课上，老师准备了三种纸片，如图1中边长分别为a、b的正方形纸片A、B ，以及长为b、宽为a的长方形纸片C ，观察图形并解答下列问题：
1. （1）小玲想用图1的三种纸片拼出一个面积为 $\text{[math]}$ 的大长方形，则需要A纸片张，B纸片张，C纸片张（空格处填写数字）
2. （2）观察图2，请写出下列三个代数式 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 之间的等量关系；
3. （3）运用你所得的公式，计算：当 $\text{[math]}$ ， $\text{[math]}$ ，请求出 $\text{[math]}$ 的值.
4. （4）现将一张A卡片放在B卡片的内部得图3，将一张A卡片和一张B卡片并列放置后构造新的正方形得图4.若图3和图4中阴影部分的面积分别为6和15，求图4的边长.
答案解析收藏纠错 + 选题
25. (2024七下·南海期中) 如图1，把一块直角三角尺 $\text{[math]}$ 的直角顶点C放置在水平直线 $\text{[math]}$ 上，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，试回答下列问题：
1. （1）若把三角尺 $\text{[math]}$ 绕着点C按顺时针方向旋转，当 $\text{[math]}$ 时， $\text{[math]}$ 度；
2. （2）在三角尺 $\text{[math]}$ 绕着点C按顺时针方向旋转过程中，分别作 $\text{[math]}$ 于M ， $\text{[math]}$ 与N ，若 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ .
3. （3）三角尺 $\text{[math]}$ 绕着点C按顺时针方向继续旋转到图3的位置，其他条件不变，则 $\text{[math]}$ 、 $\text{[math]}$ 与 $\text{[math]}$ 之间有什么关系？请说明理由.
答案解析收藏纠错 + 选题

试卷信息