一、选择题 (每小题 3 分, 共 30 分
-
A . 某班级学生的视力水平
B . 端午节期间市场上粽子的质量情况
C . 新城河的水质情况
D . 一批日光灯的使用寿命
-
-
-
-
5.
(2024七下·慈溪期末)
学校组织调查了本校若干名学生喜爱的体育活动, 制成如图所示的扇形统计图. 已知喜爱篮球的人数是 15 人,则喜爱打羽毛球的学生人数是 (

)

A . 30
B . 40
C . 60
D . 80
-
-
A . 当  时,分式有意义
B . 当
时,分式有意义
B . 当  时,
时,  C . 当
C . 当  时,
时,  D . 当
D . 当  时,
时,  越大,
越大,  的值越接近于 1
的值越接近于 1
-
8.
(2024七下·慈溪期末)
小慈和小溪两人同时从甲地出发, 骑自行车前往乙地, 已知甲乙两地的距离为

,
,并且小慈比小溪先到 18 分钟. 若设小溪每小时走

,所列方程为

,则横线上的信息可能是 (

)
A . 小慈每小时比小溪少骑行  B . 小慈每分钟比小溪多骑行
B . 小慈每分钟比小溪多骑行  C . 小慈和小溪每小时共骑行
C . 小慈和小溪每小时共骑行  D . 小慈的速度是小溪的 3 倍
D . 小慈的速度是小溪的 3 倍
-
9.
(2024七下·慈溪期末)
如图,有

型、

型、

型三种不同的纸板. 其中

型是边长为

的正方形,共有 2 块;

型是长为

,宽为

的长方形,共有 4 块;

型为边长为

的正方形,共有 3 块. 现用这 9 块纸板去拼出一个大的长方形 (不重叠、不留空隙), 则下列操作可行的是 ( )

A . 用全部 9 块纸板
B . 拿掉 1 块  型纸板
C . 拿掉 1 块 B 型纸板
D . 加上 1 块
型纸板
C . 拿掉 1 块 B 型纸板
D . 加上 1 块  型纸板
型纸板
-
A . 2024
B . 6072
C . -2024
D . -6072
二、填空题 (每小题 3 分, 共 18 分
-
-
-
13.
(2024七下·慈溪期末)
已知一组数据有 40 个, 分成六组, 第一组到第四组的频数分别为

,第五组的频率是 0.2, 则第六组的频数是
.
-
-
15.
(2024七下·慈溪期末)
如图,把数量相同的花种撒播在甲、乙两块土地上 (阴影部分),若

,则甲、乙两块土地的撤播密度的比为
. (撒播密度

)

-
16.
(2024七下·慈溪期末)
将三张边长分别为

的正方形纸片

按图 1,图 2 两种不同方式摆放于两个长方形中. 设图 1 中的阴影部分周长为

,面积为

,图 2 中的阴影部分周长为

,面积为

.若

,则

.

三、解答题 (第 17 题 6 分, 第 18、19、20、21 题各 8 分, 第 22 题 10 分, 第 23、24 题各 12 分, 共 72 分
-
17.
(2024七下·慈溪期末)
小明在计算

时,解答过程如下:
a(2+a)-(a-2)2
=2a+a2-(a2-4)…第一步
=2a+a2-a2-4…第二步
=2a-4…第三步
小明的解答从第 _▲_步开始出错,请写出正确的解答过程.
-
-
(1)
化简:

;
-
(2)
解方程组:

.
-
-
-
(1)
求

的值:
-
(2)
求

的值.
-
21.
(2024七下·慈溪期末)
校团委开展了消防知识普及活动, 并对全校 2000 名学生进行了消防知识检测, 随机抽取部分学生的答题情况, 绘制成如图的统计图 (部分). 请根据调查的信息, 解答下列问题:

-
-
-
(3)
请估计该校学生答对 9 道 (含 9 道) 以上的人数.
-
-
(1)
判定

与

的位置关系,并说明理由:
-
(2)
若

,求
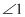
的度数.
-
23.
(2024七下·慈溪期末)
根据以下素材, 解决问题:
题:
因收纳需要,常常会准备一些无盖纸盒,现将长为8,宽为4的长方形彩纸进行裁剪,用来装饰竖式、横式的无盖纸盒.装饰竖式、横式的无盖纸盒.
 |
| 素材1 | 彩纸的裁剪方案:
 |
| 素材2 | 1个竖式无盖纸盒所需彩纸
 | 1个横式无盖纸盒所需彩纸
 |
问题解决:
-
(1)
现有彩纸 17 张, 若只装饰竖式无盖纸盒, 选用素材 1 中的两种裁剪方案, 要 求裁剪无余料, 且 17 张彩纸裁剪所得的纸片恰好全部用完, 则应选择的两种裁剪 方案是_▲_,一共可以做成多少只竖式无盖纸盒?请写出你的解答过程.
-
(2)
若装饰竖式和横式两种无盖纸盒共 2022 个, 选用素材 1 中的两种裁剪方案, 要求裁剪后无余料, 且裁剪所得的纸片恰好全部用完, 则至少需要多少张彩纸?
-
24.
(2024七下·慈溪期末)
小磊和小轩在课外练习中碰到了一个问题,需要对多项式

进行因式分解. 小磊认为该整式一定有一个因式

,小轩认为必有因式是

,两人找到老师寻求帮助. 老师提供了一个方法: 因式分解是整式乘法的逆运算. 若整式

能被整式

整除,则

必为

的一个因式. 老师给出了演算方法:

-
(1)
观察老师的演算后,你认为 同学的想法是对的;
-
(2)
已知多项式

的其中一个因式为

,请试着根据老师的方法列出演算过程,并将多项式

进行因式分解;
-
(3)
若多项式

能因式分解成

与另一个完全平方式,求

与

的值.







