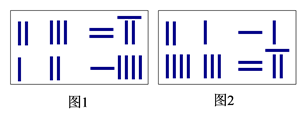
类似地，图2所示的算筹图我们可以表述为（ ）
方程①：
第一步方程②：
第二步方程③：
其实以上步骤的本质就是在消元，根据以上操作，有下列结论：（1）数列M为：（2）
（3）
其中正确的有（ ）
大意是：李白在郊外春游时，做出这样一条约定：遇见朋友，先到酒店里将壶里的酒增加一倍，再喝掉其中的5升酒.按照这样的约定，在第3个店里遇到朋友正好喝光了壶中的酒.则李白的酒壶中原有升酒.
《张丘建算经》是一部数学问题集，其内容、范围与《九章算术》相仿．其中提出并解决了一个在数学史上非常著名的不定方程问题，通常称为“百鸡问题”：“今有鸡翁一值钱五，鸡母一值钱三，鸡雏三值钱一，凡百钱买鸡百只，问鸡翁、母、雏各几何．”
译文：公鸡每只值五文钱，母鸡每只值三文钱，小鸡每三只值一文钱，现在用一百文钱买一百只鸡，问这一百只鸡中，公鸡、母鸡、小鸡各有多少只？结合你学过的知识，解决下列问题：
①则小鸡有只，买小鸡一共花费文钱；（用含x，y的式子表示）
②根据题意列出一个含有x，y的方程：；
今携一壶酒，游春郊外走．逢朋加一倍，入店饮半斗．相逢三处店，饮尽壶中酒．试问能算士：如何知原有．
注：古代一斗是10升．
大意是：李白在郊外春游时，做出这样一条约定：遇见朋友，先到酒店里将壶里的酒增加一倍，再喝掉其中的5升酒．按照这样的约定，在第3个店里遇到朋友正好喝光了壶中的酒．
用含an﹣1的式子表示an=，再用含a0和n的式子表示an=；
我国明朝数学家程大位所著的《算法统宗》中介绍了一种计算乘法的方法，称为“铺地锦”如图1所示，计算31×47，首先把乘数31和47分别写在方格的上面和右面，然后以31的每位数字分别乘以47的每位数字，将结果计入对应的格子中（如图1，12写在3下面的方格里，十位1写在斜线的上面，个位2写在斜线的下面），再把同一斜线上的数相加，结果写在斜线末端，最后把得数依次写下来时1457，即31×47=1457．如图2，计算46×71，将乘数46写在方格上边，乘数71写在方格右边，然后用乘数46的每位数字乘以乘数71的每位数字，将结果计入相应的方格中，最后沿斜线方向相加得3266．
名句“运筹帷幄之中，决胜千里之外”中的“筹”原意是指“算筹”，在我国古代的数学名著《九章算术》和《孙子算经》（如图1）中都有记载．“算筹”是古代用来进行计算的工具之一，它是将几寸长的小竹棍摆在平面上进行运算，“算筹”的摆放有纵、横两种形式（如图2）．当表示一个多位数时，要像阿拉伯计数一样，把各数位的数码从左到右排列，但各数位数码的摆放需要纵横相间：个位、百位、万位数用纵式表示，十位、千位、十万位数用横式表示，“0”用空位来代替，例如：2307用“算筹”表示就是
， 而《九章算术》中“方程”一章介绍了用“算筹图”解决二元一次方程组的方法，例如
， 在从左到右的符号中，前两个符号分别代表未知数的系数，后两个符号表示对应的常数项，则根据此图可以列出方程
任务：
表示的数是．
， 列出方程组并求解．
