一、单项选择题(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
-
-
-
A . 0
B . 1
C .  D .
D . 
-
-
-
-
A . 充分不必要条件
B . 必要不充分条件
C . 充要条件
D . 既不充分也不必要条件
-
8.
(2024高二上·丰城开学考)
在棱长为3的正方体

中,点Р是侧面

上的点,且点Р到棱

与到棱AD的距离均为1,用过点Р且与

垂直的平面去截该正方体,则截面在正方体底面ABCD的投影多边形的面积是( )
A .  B . 5
C .
B . 5
C .  D . 8
D . 8
二、多项选择题(本大题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对得6分,部分选对的得部分,有选错的得0分)
-
A . 函数 在
在 处有极大值
B . 函数
处有极大值
B . 函数 在区间
在区间 上是增函数
C . 函数
上是增函数
C . 函数 在
在 有极大值
D . 函数
有极大值
D . 函数 在区间
在区间 和
和 上是增函数
上是增函数
-
A .  B . 有序数对
B . 有序数对 有6个
C .
有6个
C .  的最小值是
的最小值是 D .
D . 
-
三、填空题(本大题共3小题,每小题5分,共15分,请把正确答案填在题中横线上)
-
-
-
14.
(2024高二上·丰城开学考)
已知椭圆

的左,右焦点分别为

, 过点

且垂直于

轴的直线与椭圆交于

两点,

分别交

轴于

两点,

的周长为6,过

作

外角平分线的垂线与直线

交于点

, 则

.
四、解答题(本大题共5小题,共77分.解答时应写出必要的文字说明,证明过程或演算)
-
-
(1)
证明:

.
-
-
-
-
(2)
若函数

有两个零点,求实数

的取值范围.
-
-
-
(2)
求数列

的通项公式;
-
(3)
设

, 证明:

.
-
18.
(2024高二上·丰城开学考)
在如图所示的试验装置中,两个正方形框架

的边长都是1,且它们所在的平面互相垂直.活动弹子

分别在正方形对角线

和

上移动,且
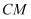
和

的长度保持相等,记

.

-
(1)
求

长的最小值;
-
(2)
当

的长最小时,求二面角

的正弦值.
-
19.
(2024高二上·丰城开学考)
已知等比数列

的公比为q(

),其所有项构成集合A,等差数列

的公差为d(

),其所有项构成集合B.令

, 集合C中的所有元素按从小到大排列构成首项为1的数列

.
-
-
(2)
若

, 数列

为无穷数列,

, 且数列

的前5项成公比为p的等比数列.当

时,求p的值;
-
(3)
若数列

是首项为1的无穷数列,求证:“存在无穷数列

, 使

”的充要条件是“d是正有理数”.