一、选择题（本大题共10小题，每小题3分，共30分．在每小题所给出的四个选项中，只有一项是正确的，只需把答案直接填写在答卷上相应的位置）
-
-
2.
(2024七上·无锡期中)
中国是最早采用正负数表示相反意义的量的国家，如果将“收入
元”记作“
元”，那么“支出
元”记作（ ）
-
-
-
-
6.
(2024七上·无锡期中)
下列说法：①
一定是负数；②一个数的绝对值一定是正数；③一个有理数不是正数就是负数；④绝对值等于本身的数是非负数，其中正确的个数是（ ）
-
A . 8
B . 2
C . 
或2
D . 8或 
-
-
9.
(2024七上·无锡期中)
用大小完全相同的圆点按如图所示的规律拼图案，其中第①个图案中有
个圆点，第②个图案中有
个圆点，第③个图案中有
个圆点，第④个图案中有
个圆点，…，按此规律排列下去，则第⑨个图案中圆点的个数为（ ）
-
10.
(2024七上·无锡期中)
将8张长为
， 宽为
的小长方形纸片，按图1和图2所示的两种方式放在长方形
内（相邻的小长方形既无重叠，又不留空隙）．图1中两块阴影部分的周长和为
， 图2中阴影部分的周长为
． 若长方形
的长比宽大
， 则
的值为（ ）
二、填空题（本大题共8小题，每小题3分，共24分；不需写出解答过程，只需把答案直接填写在答题卡上相应的位置）
三、解答题（本大题共8小题，共66分．请在答题卡指定区城内作答，解答时应写出文字说明、证明过程成演算步票）
-
19.
(2024七上·无锡期中)
把下列各数的序号分别填入相应的集合内：①
， ②
， ③
， ④
， ⑤
， ⑥
， ⑦
， ⑧
， ⑨
．
整数集合_______________…；
正分数集合_______________…；
非正数集合_______________…．
-
-
-
（1）
-
（2）
-
-
（1）
求
；
-
-
23.
(2024七上·无锡期中)
最近几年时间，全球的新能源汽车发展迅猛，尤其对于我国来说，新能源汽车产销量都大幅增加．小明家新换了一辆新能源纯电动汽车，他连续
天记录了每天行驶的路程：
，
，
，
，
，
，
． 以
为标准，多于
的记为“
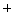
”，不足
的记为“
”，刚好
的记为“
”．
-
（1）
这
天里路程最多的一天比最少的一天多走________
；
-
（2）
请求出小明家的新能源汽车这七天一共行驶了多少千米？
-
（3）
已知汽油车每行驶
需用汽油
升，汽油价
元/升，而新能源汽车每行驶
耗电量为
度，每度电为
元，请估计小明家换成新能源汽车后这
天的行驶费用比原来节省多少钱？
-
24.
(2024七上·无锡期中)
如图，某社区要在两块紧挨在一起的长方形荒地上修建一个半圆形花圃，其余荒地（阴影部分）绿化种草皮，尺寸如图所示（单位：米）
-
（1）
求草皮的种植面积（结果保留
， 用含
的代数式表示）；
-
-
-
（1）
根据定义，填空：
________；
________．
-
（2）
若有如下运算性质：
，
根据运算性质填空：
若
， 则
________；
________．
-
（3）
表中与数
对应的
有且只有两个是错误的，请找出错误，说明理由并改正．
-
26.
(2024七上·无锡期中)
已知有理数
，
满足：
． 如图，在数轴上，点
是原点，点
所对应的数是
， 线段
在直线
上运动（点
在点
的左侧），
-
（1）
________，
________；
-
-
（3）
在线段
运动过程中，若
为线段
的中点，
为线段
的中点，则线段
的长度是定值吗？若是，请求出这个定值，若不是，请说明理由．
四、附加题
-
27.
(2024七上·无锡期中)
材料一：杨辉三角两腰上的数都是
， 其余每个数为它的上方（左右）两数之和，揭示了
（
为非负整数）展开式的项数及各项系数的相关规律，运用规律可以解决很多数学问题．材料二：斐波那契数列是意大利数学家菜昂纳多—斐波那契从兔子繁殖问题中引入的一列神奇数字，用
表示这一列数中的第
个，则数列为
，
，
，
，
， …，数列从第三项开始，每一项都等于其前两项之和，即
（
为正整数）．结合材料，回答以下问题：
-
（1）
多项式
展开式共有________项，各项系数和为________，利用展开式规律计算：
________；
-
（2）
我们借助杨辉三角中第三斜行的数：
，
，
， 10，…记
，
，
，
， …则
________；
________（用
表示）：
________．
-
（3）
如图2，把杨辉三角左对齐排列，将同一条斜线上的数字求和，计算可得
，
，
，
，
，
， …若
， 且
， 结合材料二，求
的值（用
表示）．
