一、选择题(本题共10小题,每小题3分,共30分.在每小题给出的选项中,只有一项是符合题目要求的)
-
-
-
A . 40°
B . 70°
C . 100°
D . 40°或100°
-
-
-
-
A . 1
B .  C . 2
D .
C . 2
D . 
-
8.
(2024八上·湘潭期中)
如图,

的平分线

, 与

的外角

的平分线相交于点F,过点F作

交

于点D,交

于点E,若

,

, 则

的长为( )

.

A . 4.5
B . 5
C . 5.5
D . 6
-
9.
(2024八上·湘潭期中)
《四元玉鉴》是中国古代著名的数学专著,书里记载一道这样的题:“今有绫、罗共三丈,各直钱八百九十六文.只云绫、罗各一尺共直钱一百二十文.问绫、罗尺价各几何?”题目译文是:现在有绫布和罗布,布长共3丈(一丈

尺),已知绫布和罗布分别全部出售后均能收入八百九十六文;绫布和罗布各出售一尺共收入一百二十文.问两种布每尺各多少钱?若设绫布有x尺,根据题意可列方程为( )
-
10.
(2024八上·沾益期末)
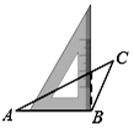
如图在第一个△A
1BC中,∠B=40°,A
1B=BC,在边A
1B上任取一点D,延长CA
1到A
2 , 使A
1A
2=A
1D,得到第二个△A
1A
2D,再在边A
2D上任取一点E,延长A
1A
2到A
3 , 使A
2A
3=A
2E,得到第3个△A
2A
3E.……如此类推,可得到第n个等腰三角形.则第n个等腰三角形中,以A
n为顶点的内角的度数为( )

二、填空题(本题共8小题,每小题3分,共24分)
-
-
-
13.
(2024八上·湘潭期中)
中国华为公司研发的麒麟

芯片是全球第一款采用

工艺制造的最先进手机处理器.已知

, 则数据“

”用科学记数法表示为
.
-
-
-
-
-
18.
(2024八上·湘潭期中)
如图,在

中,

,

,

的面积是16,

边的垂直平分线

分别交

,

边于点E,F.若点D为

边的中点,点M为线段EF上一动点,则

周长的最小值为
.

三、计算题(本大题共2小题,共12分。)
四、解答题(本题共2小题,共16分。解答应写出文字说明,证明过程或演算步骤。)
-
-
(1)
求证:

;
-
-
五、解答题(本题共2小题,共18分。解答应写出文字说明,证明过程或演算步骤。)
-
-
(1)
求

的度数;
-
(2)
求证:

是等边三角形.
-
24.
(2024八上·湘潭期中)
列方程解应用题:
某商场用8万元购进一批新款衬衫,上架后很快销售一空,商场又紧急购进第二批这种衬衫,数量是第一次的2倍,但进价涨了4元/件,结果共用去17.6万元.
(1)该商场第一批购进衬衫多少件?
(2)商场销售这种衬衫时,每件定价都是58元,剩至150件时按八折出售,全部售完.售完这两批衬衫,商场共盈利多少元?
六、解答题(本题共2小题,共20分。解答应写出文字说明,证明过程或演算步骤。)
-
-
(1)
如图1,求证:

是等腰三角形.
-
-
(3)
如图3,延长

,

交于点

, 求证:点

在

的垂直平分线上.
-
-
(1)
分式

是分式

的“
差分式”.
-
(2)
分式

是分式

的“

差分式”.
① (含
(含 的代数式表示);
的代数式表示);
②若 的值为正整数,
的值为正整数, 为正整数,求
为正整数,求 的值.
的值.
-
(3)
已知

, 分式

是

的“

差分式”(其中

为正数),求

的值.
 B .
B .  C .
C . 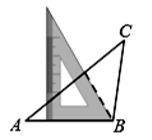 D .
D . 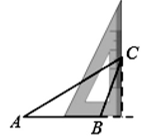

(含
的代数式表示);
的值为正整数,
为正整数,求
的值.