2015-2016学年吉林省长春市农安三中九年级下学期期中数...

由5个相同的小正方体组成的几何体如图所示，这个几何体的主视图是（  ）

如图，在△ABC中，DE∥BC交AB于点D，交AC于点E．若AB=4，AC=3，AD=3，则AE的长为（  ）

如图，点C在以AB为直径的⊙O上（点C不与A、B重合），点E在弦AC上，EF⊥AB于点F，若∠B=66°，则∠AEF的大小为（  ）

如图，在平面直角坐标系中，抛物线y=a（x﹣3）²+2（a＞0）的顶点为A，过点A作y轴的平行线交抛物线y=﹣ x²﹣2于点B，则A、B两点间的距离为．

如图，为了测量某交通路口设立的路况显示牌的立杆AB的高度，在D处用高1.2m的测角仪CD，测得最高点A的仰角为32°，已知观测点D到立杆AB的距离DB为3.8m，求立杆AB的高度．（结果精确到0.1m）

【参考数据：sin32°=0.53，cos32°=0.85，tan32°=0.62】

在Rt△ABC中，∠ACB=90°，D、E分别为边AB、BC的中点，点F在边AC的延长线上，∠FEC=∠B，求证：四边形CDEF是平行四边形．

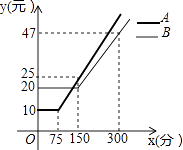
某通讯公司推出A、B两种手机话费套餐，这两种套餐每月都有一定的固定费用和免费通话时间，超过免费通话时间的部分收费标准为：A套餐a元/分，B套餐b元/分，使用A、B两种套餐的通话费用y（元）与通话时间x（分）之间的函数图象如图所示．

在Rt△ABC中，∠ACB=90°，AC=BC，D为边AB中点，点E、F分别在射线CA、BC上，且AE=CF，连结EF．

猜想：如图①，当点E、F分别在边CA和BC上时，线段DE与DF的大小关系为                          ．

探究：如图②，当点E、F分别在边CA、BC的延长线上时，判断线段DE与DF的大小关系，并加以证明．

应用：如图②，若DE=4，利用探究得到的结论，求△DEF的面积．

如图，在平面直角坐标系中，抛物线y=﹣x²+mx（m＞0且m≠1）与x轴交于原点O和点A，点B的坐标为（1，﹣1），连结AB，将线段AB绕点A顺时针旋转90°得到线段AC，连结OB、OC．

如图，在Rt△ABC中，∠C=90°，AC=BC=4，点P从点C出发沿CA以每秒1个单位长度的速度向终点A运动：同时，点Q从点C出发沿CB﹣BA运动，点Q在CB上的速度为每秒2个单位长度，在BA上的速度为每秒 个单位长度，当点P到达终点A时，点Q随之停止运动．以CP、CQ为邻边作▱CPMQ，设▱CPMQ与△ABC重叠部分图形的面积为y（平方单位），点P的运动时间为x（秒）．