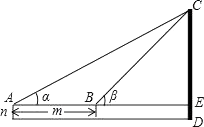
82 [
]=9
[
]=3
[
]=1,这样对82只需进行3次操作后变为1,类似地,对121只需进行多少次操作后变为1( )
①若a+b+c=0,则b2﹣4ac>0;②若方程两根为﹣1和2,则2a+c=0;③若方程ax2+c=0有两个不相等的实根,则方程ax2+bx+c=0必有两个不相等的实根;④若b=2a+c,则方程有两个不相等的实根.其中正确的有( )
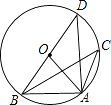

 B .
B .  C .
C .  D .
D . 
![]()