1. (2021八上·武侯期末) [阅读理解]

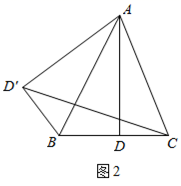
如图，在△ABC中，AB＝4，AC＝6，BC＝7，过点A作直线BC的垂线，垂足为D，求线段AD的长.

解：设BD＝x，则CD＝7﹣x.

∵AD⊥BC，

∴∠ADB＝∠ADC＝90°.

在Rt△ABD中，AD²＝AB²﹣BD² ，

在Rt△ACD中，AD²＝AC²﹣CD² ，

∴AB²﹣BD²＝AC²﹣CD².

又∵AB＝4，AC＝6，

∴4²﹣x²＝6²﹣（7﹣x）².

解得x＝ ，

∴BD＝ .

∴AD＝ ＝ .

[知识迁移]

1. （1） 在△ABC中，AB＝13，AC＝15，过点A作直线BC的垂线，垂足为D.

   i）如图1，若BC＝14，求线段AD的长；

   ii）若AD＝12，求线段BC的长.

3. （2） 如图2，在△ABC中，AB＝ ，AC＝ ，过点A作直线BC的垂线，交线段BC于点D，将△ABD沿直线AB翻折后得到对应的△ ，连接CD′，若AD＝ ，求线段 的长.