【培优版】北师大版数序八上第一章勾股定理单元测试卷

更新时间：2024-07-11 浏览次数：57 类型：单元试卷

一、选择题 (本大题共 8 小题, 每小题 3 分, 共 24 分, 每小题有四个选项, 其中只有一个是正确的）

1. (2023八上·瓯海期中) 如图，在 $\text{[math]}$ 中，边 $\text{[math]}$ 的垂直平分线分别交 $\text{[math]}$ ， $\text{[math]}$ 于点 $\text{[math]}$ ， $\text{[math]}$ ，边 $\text{[math]}$ 的垂直平分线分别交 $\text{[math]}$ ， BC于点N ， F ， $\text{[math]}$ 的周长为9.若 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的面积为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . 5 D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2021八上·西安月考) 如图，凸四边形 $\text{[math]}$ 中， $\text{[math]}$ ，若点M、N分别为边 $\text{[math]}$ 上的动点，则 $\text{[math]}$ 的周长最小值为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . 6 D . 3

答案解析收藏纠错 + 选题
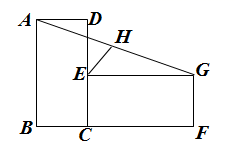
3. (2021八下·营口期末) 矩形ABCD与ECFG如图放置，点B ， C ， F共线，点C ， E ， D共线，连接AG ，取AG的中点H，连接EH ．若 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ （）

A . $\text{[math]}$ B . 2 C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
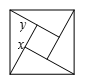
4. (2017八上·郑州期中) 如图使用4个全等三角形与1个小正方形镶嵌而成的正方形图案已知大正方形面积为49，小正方形面积为4，若用x、y表示直角三角形的两直角边(x>y)，下列四个说法：①x²+y²=49；②x−y=2；③2xy+4=49；④x+y=9. 其中正确的是（）

A . ①② B . ①②③ C . ①②④ D . ①②③④

答案解析收藏纠错 + 选题
5. (2016八上·高邮期末) 如图，Rt△ABC，∠ACB=90°，AC=3，BC=4，将边Ac沿CE翻折，使点A落在AB上的D处，再将边BC沿CF翻折，使点B落在CD的延长线上的点F处，两条折痕与斜边AB分别交于点E、F，则线段BF的长为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6.
如图，在△ABC中，AB=AC=5，P是BC边上除B、C点外的任意一点，则代数式AP²+PB•PC等于（　　）

A . 25 B . 15 C . 20 D . 30

答案解析收藏纠错 + 选题
7.
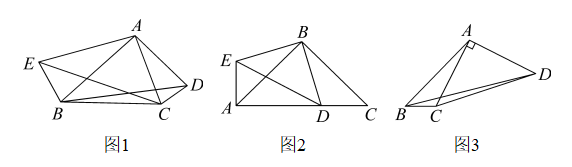
图1为一个长方体，AD=AB=10，AE=6，M，N为所在棱的中点，图2为图1的表面展开图，则图2中MN的长度为（　　）

A . 11 $\text{[math]}$ B . 10 $\text{[math]}$ C . 10 D . 8

答案解析收藏纠错 + 选题
8. (2021八上·萧山期末) 已知等腰三角形 $\text{[math]}$ ， $\text{[math]}$ ，点 $\text{[math]}$ 是 $\text{[math]}$ 上一点，若 $\text{[math]}$ ， $\text{[math]}$ .则 $\text{[math]}$ 的周长可能是（）

A . 15 B . 20 C . 28 D . 36

答案解析收藏纠错 + 选题

二、填空题（本大题共5小题, 每小题3分, 共15分)

9. (2024八上·滨江期末) 如图，有一直角三角形纸片 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 于点 $\text{[math]}$ ． $\text{[math]}$ ， $\text{[math]}$ 分别是线段 $\text{[math]}$ ， $\text{[math]}$ 上的点， $\text{[math]}$ ， Ⅰ分别是线段 $\text{[math]}$ ， $\text{[math]}$ 上的点，沿 $\text{[math]}$ ， $\text{[math]}$ 折叠，使点 $\text{[math]}$ ， $\text{[math]}$ 恰好都落在线段 $\text{[math]}$ 上的点 $\text{[math]}$ 处．当 $\text{[math]}$ 时， $\text{[math]}$ 的长是．

答案解析收藏纠错 + 选题
10. (2024八上·龙泉驿期末) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 为 $\text{[math]}$ 外一点，连接 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，发现 $\text{[math]}$ ， $\text{[math]}$ 且 $\text{[math]}$ ，则 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
11. (2024八上·武侯月考) 在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，点D在线段 $\text{[math]}$ 上从点C向点B移动，同时，点E在线段 $\text{[math]}$ 上由点A向点B移动，当点D与点B重合时运动停止，已知它们的运动速度相同，连接 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的最小值为．

答案解析收藏纠错 + 选题
12. (2023·期中) 商场卫生间旋转门锁的局部图如图1所示，图2是其工作简化图．其中OD＝3.5cm，在自然状态下，把手竖直向下（把手底端到达A处）．旋转一定角度，使得把手底端B恰好卡在门边，此时底端A，B的竖直高度差为0.5cm，则OB的长度是 cm．当把手旋转到OC⊥OB时，点C与点B的高度差BH是 cm．

答案解析收藏纠错 + 选题
13. (2023八上·杭州期中) 如图，已知等边△ABC的边长为4，点P是边BC上一点，BP＝1，则AP＝，若点Q是边AC上一点，BQ＝AP ，则AQ＝．

答案解析收藏纠错 + 选题

三、解答题（共7题；共61分）

14. (2019八上·抚州月考) 如图1，在 $\text{[math]}$ 的网格纸中，每个小正方形的边长都为1，动点P、Q分别从点D、A同时出发向右移动，点P的运动速度为每秒2个单位，点Q的运动速度为每秒1个单位，当点P运动到点C时，两个点都停止运动.
1. （1）请在 $\text{[math]}$ 的网格纸图2中画出运动时间t为2秒时的线段PQ并求其长度；
2. （2）在动点P、Q运动的过程中，△PQB能否成为PQ=BQ的等腰三角形？若能，请求出相应的运动时间t；若不能，请说明理由；
3. （3）在（1）中的图2中，点E如图所示，是否在PQ上存在一点M，使DM+EM的值最小，如存在，求出DM+EM最小值；如不存在，说明理由.
答案解析收藏纠错 + 选题
15. (2022八下·广元月考) 长方体的长为20cm，宽为10cm，高为15cm，点B离点C5cm，一只蚂蚁如果要沿着长方体的表面从点A爬到点B去吃一滴蜜糖，需要爬行的最短距离是多少？

答案解析收藏纠错 + 选题
16. (2018八上·汽开区期末) 在△ABC中，∠BAC=90°，AB=AC.点D为直线BC上一动点（点D不与点B、C重合），以AD为直角边在AD右侧作等腰直角三角形ADE，使∠DAE=90°，连结CE.
1. （1）探究：如图①，当点D在线段BC上时，证明BC=CE+CD.
2. （2）应用：在探究的条件下，若AB= $\text{[math]}$ ，CD=1，则△DCE的周长为.
3. （3）拓展：①如图②，当点D在线段CB的延长线上时，BC、CD、CE之间的数量关系为.
  ②如图③，当点D在线段BC的延长线上时，BC、CD、CE之间的数量关系为.
答案解析收藏纠错 + 选题
17. (2021八上·武侯期末) [阅读理解]
如图，在△ABC中，AB＝4，AC＝6，BC＝7，过点A作直线BC的垂线，垂足为D，求线段AD的长.

解：设BD＝x，则CD＝7﹣x.

∵AD⊥BC，

∴∠ADB＝∠ADC＝90°.

在Rt△ABD中，AD²＝AB²﹣BD² ，

在Rt△ACD中，AD²＝AC²﹣CD² ，

∴AB²﹣BD²＝AC²﹣CD².

又∵AB＝4，AC＝6，

∴4²﹣x²＝6²﹣（7﹣x）².

解得x＝ $\text{[math]}$ ，

∴BD＝ $\text{[math]}$ .

∴AD＝ $\text{[math]}$ ＝ $\text{[math]}$ .

[知识迁移]
1. （1）在△ABC中，AB＝13，AC＝15，过点A作直线BC的垂线，垂足为D.
  i）如图1，若BC＝14，求线段AD的长；
  
  ii）若AD＝12，求线段BC的长.
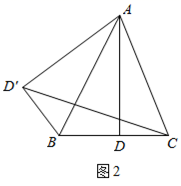
2. （2）如图2，在△ABC中，AB＝ $\text{[math]}$ ，AC＝ $\text{[math]}$ ，过点A作直线BC的垂线，交线段BC于点D，将△ABD沿直线AB翻折后得到对应的△ $\text{[math]}$ ，连接CD′，若AD＝ $\text{[math]}$ ，求线段 $\text{[math]}$ 的长.
答案解析收藏纠错 + 选题
18. (2023八上·乐山期末)
1. （1）【问题情境】课外兴趣小组活动时，老师提出了如下问题：如图①， $\text{[math]}$ 中，若 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 边上的中线 $\text{[math]}$ 的取值范围．小明经过组内合作交流，得到了如下的解决方法：延长 $\text{[math]}$ 至点 $\text{[math]}$ ，使 $\text{[math]}$ ，连接 $\text{[math]}$ ．请根据小明的方法思考：
  ①由已知和作图能得到 $\text{[math]}$ ，依据是     ▲     ．
  A． $\text{[math]}$     B． $\text{[math]}$     C． $\text{[math]}$     D． $\text{[math]}$
  ②由“三角形的三边关系”可求得 $\text{[math]}$ 的取值范围是     ▲  ．
2. （2）【初步运用】
  如图②， $\text{[math]}$ 是 $\text{[math]}$ 的中线， $\text{[math]}$ 交 $\text{[math]}$ 于 $\text{[math]}$ ，交 $\text{[math]}$ 于 $\text{[math]}$ ，且 $\text{[math]}$ ，若 $\text{[math]}$ ， $\text{[math]}$ ，求线段 $\text{[math]}$ 的长．
3. （3）【灵活运用】
  如图③，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ 为 $\text{[math]}$ 中点， $\text{[math]}$ ， $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ， $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ，连接 $\text{[math]}$ ．若 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的长度．
答案解析收藏纠错 + 选题
19. (2023八上·泉州期末)
1. （1）观察猜想，如图①点B、A、C在同一条直线上，DB⊥BC，EC⊥BC且∠DAE＝90°，AD＝AE，则BC、BD、CE之间的数量关系为；
2. （2）问题解决，如图②，在Rt△ABC中，∠ABC＝90°，CB＝6，AB＝3，以AC为直角边向外作等腰Rt△DAC，连结BD，求BD的长；
3. （3）拓展延伸，如图③，在四边形ABCD中，∠ABC＝∠ADC＝90°，CB＝6，AB＝3，DC＝DA，请直接写出BD的长.
答案解析收藏纠错 + 选题
20. (2021八上·双阳期末) 解答
1. （1）【问题探究】
  如图1，锐角△ABC中分别以AB、AC为边向外作等腰△ABE和等腰△ACD，使AE=AB，AC＝AD，∠ABE＝∠ADC，连接EC，BD．求证：EC＝BD．
2. （2）【拓展延伸】
  ①如图2，△ABC中，∠ABC＝90°，CB＝AB，D为AC上一点，连结BD，作BE⊥BD，AE⊥AC，连结DE．若AC＝2，请直接写出四边形ADBE的面积．
  ②如图3，四边形ABCD中，AD⊥AC，AC＝AD，∠ABC＝45°，AB＝3，BC＝1，请直接写出BD长．
答案解析收藏纠错 + 选题