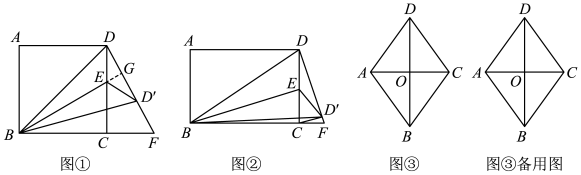
如图①,已知四边形ABCD是正方形,点E为CD边上一点(不与端点重合),连接BE,作点D关于BE的对称点D',DD'的延长线与BC的延长线交于点F,连接BD′,D'E.
①小明探究发现:当点E在CD上移动时,△BCE≌△DCF.并给出如下不完整的证明过程,请帮他补充完整.
证明:延长BE交DF于点G.
②进一步探究发现,当点D′与点F重合时,∠CDF= ▲ °.
如图②,四边形ABCD为矩形,点E为CD边上一点,连接BE,作点D关于BE的对称点D',DD′的延长线与BC的延长线交于点F,连接BD',CD',D'E.当CD'⊥DF,AB=2,BC=3时,求CD'的长;
如图③,已知四边形ABCD为菱形,AD= , AC=2,点F为线段BD上一动点,将线段AD绕点A按顺时针方向旋转,当点D旋转后的对应点E落在菱形的边上(顶点除外)时,如果DF=EF,请直接写出此时OF的长.
微信扫码预览、分享更方便