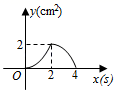
 B .
B . 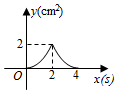 C .
C . 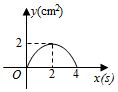 D .
D . 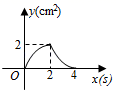





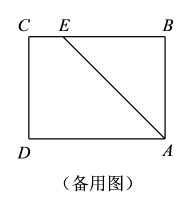


(备用图)


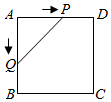
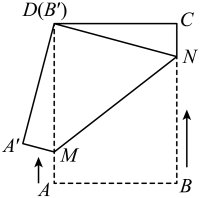
如图,已知矩形ABCD的边长AB=3cm , BC=6cm . 某一时刻,动点M从A点出发沿AB方向以1cm/s的速度向B点匀速运动;同时,动点N从D点出发沿DA方向以2cm/s的速度向A点匀速运动,是否存在时刻t , 使以A , M , N为顶点的三角形与△ACD相似?若存在,直接写出t的值;若不存在,请说明理由.

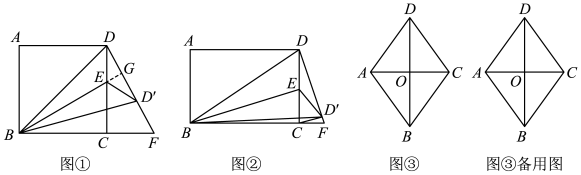
如图①,已知四边形ABCD是正方形,点E为CD边上一点(不与端点重合),连接BE,作点D关于BE的对称点D',DD'的延长线与BC的延长线交于点F,连接BD′,D'E.
①小明探究发现:当点E在CD上移动时,△BCE≌△DCF.并给出如下不完整的证明过程,请帮他补充完整.
证明:延长BE交DF于点G.
②进一步探究发现,当点D′与点F重合时,∠CDF= ▲ °.
如图②,四边形ABCD为矩形,点E为CD边上一点,连接BE,作点D关于BE的对称点D',DD′的延长线与BC的延长线交于点F,连接BD',CD',D'E.当CD'⊥DF,AB=2,BC=3时,求CD'的长;
如图③,已知四边形ABCD为菱形,AD= , AC=2,点F为线段BD上一动点,将线段AD绕点A按顺时针方向旋转,当点D旋转后的对应点E落在菱形的边上(顶点除外)时,如果DF=EF,请直接写出此时OF的长.

若四边形是菱形,
, 点P是射线BD上一动点,以
为边向右侧作等边
, 如图1,当点E在菱形
内部或边上时,连接
, 则BP与
有怎样的数量关系?并说明理由;
若四边形是正方形,点P是射线BD上一动点,以
为直角边在
边的右侧作等腰
, 其中
, 如图2.当点P在对角线BD上,点E恰好在
边所在直线上时,则BP与
之间的数量关系?并说明理由;
在(2)的条件下,如图3,在正方形中,
, 当P是对角线BD的延长线上一动点时,连接BE,若
, 求
的面积.

如图①,正方形AEFG的两边分别在正方形ABCD的边AB和AD上,连接CF .
填空:①线段CF与DG的数量关系为;
②直线CF与DG所夹锐角的度数为.
如图②,将正方形AEFG绕点A逆时针旋转,在旋转的过程中,(1)中的结论是否仍然成立,请利用图②进行说明.
如图③,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,AB=AC=4,O为AC的中点.若点D在直线BC上运动,连接OE , 则在点D的运动过程中,线段OE长的最小值为(直接写出结果).