
 B .
B .  C .
C .  D .
D . 

小张:该工艺品的进价是每个22元;
小李:当销售价为每个38元时,每天可售出160个;当销售价降低3元时,平均每天将能多售出120个.
经理:为了实现平均每天3640元的销售利润,这种工艺品的销售价应降低多少元?
设这种工艺品的销售价每个应降低x元,由题意可列方程为( )
x | … | ﹣4 | ﹣3 | ﹣2 | ﹣1 | ﹣0.5 | 0.5 | 1 | b | 3 | 4 | … |
y | … | ﹣1 | ﹣ | a | ﹣4 | ﹣8 | 8 | 4 | 2 | 1 | … |
表格中,a=,b=;
②若(x1 , y1),(x2 , y2)在该函数的图象上,且x1<x2<0,则y1y2(填“>”,“=”或“<”).
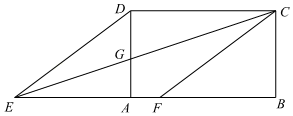

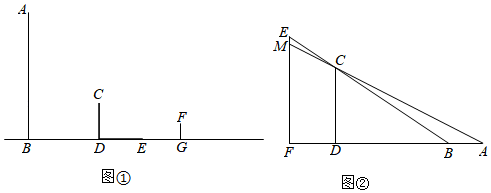
①根据光源确定榕树在地面上的影子;
②测量出相关数据,如高度,影长等;
③利用相似三角形的相关知识,可求出所需要的数据.
根据上述内容,解答下列问题:
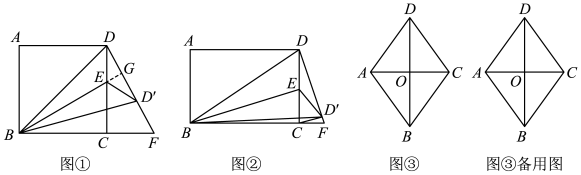
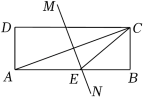
如图①,已知四边形ABCD是正方形,点E为CD边上一点(不与端点重合),连接BE,作点D关于BE的对称点D',DD'的延长线与BC的延长线交于点F,连接BD′,D'E.
①小明探究发现:当点E在CD上移动时,△BCE≌△DCF.并给出如下不完整的证明过程,请帮他补充完整.
证明:延长BE交DF于点G.
②进一步探究发现,当点D′与点F重合时,∠CDF= ▲ °.
如图②,四边形ABCD为矩形,点E为CD边上一点,连接BE,作点D关于BE的对称点D',DD′的延长线与BC的延长线交于点F,连接BD',CD',D'E.当CD'⊥DF,AB=2,BC=3时,求CD'的长;
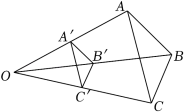
如图③,已知四边形ABCD为菱形,AD= , AC=2,点F为线段BD上一动点,将线段AD绕点A按顺时针方向旋转,当点D旋转后的对应点E落在菱形的边上(顶点除外)时,如果DF=EF,请直接写出此时OF的长.