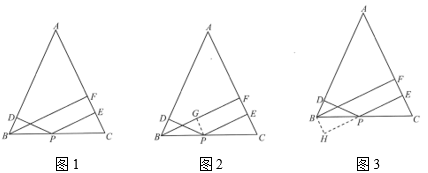
某“数学学习兴趣小组”在学习了“等腰三角形的性质”和“平行四边形的性质和判定”后,在习题中发现了这样一个问题:如图1,在等腰中,
, 点D、E分别是边
上的点,点P是底边
上的点,且
, 过点B作
于点F,请写出线段
、
、
之间满足的数量关系式.
同学们经过交流讨论,得到了如下两种解决思路:
解决思路1:如图2,过点P作于点G;
解决思路2:如图3,过点B作 , 交
的延长线于点H;
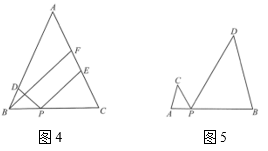
如图4,在等腰中,
, 点D、E分别是边
上的点,点P是底边
上的点,且
, 过点B作
交
于点F,请写出线段
之间满足的数量关系式,并说明理由.
如图5,在与
中,
,
, 点A、B、P在同一条直线上,若
,
, 则
.