辽宁省大石桥市水源镇九年一贯制学校2017-2018学年九年...

更新时间：2024-07-13 浏览次数：329 类型：期末考试

一、单选题

1. (2018九上·大石桥期末) 已知一个直角三角形的两条直角边的长恰好是方程x²－3x＝4(x－3)的两个实数根，则该直角三角形斜边上的中线长是（）

A . 3 B . 4 C . 6 D . 2.5

答案解析收藏纠错 + 选题
2. (2023九上·恩施期中) 下列4个图形中，是中心对称图形但不是轴对称的图形是（）

A . B . C . D .

答案解析收藏纠错 + 选题
3. (2018九上·大石桥期末) 把抛物线y＝ $\text{[math]}$ x²－1先向右平移1个单位，再向下平移2个单位，得到的抛物线的解析式为（）

A . y＝ $\text{[math]}$ (x＋1)²－3 B . y＝ $\text{[math]}$ (x－1)²－3 C . y＝ $\text{[math]}$ (x＋1)²＋1 D . y＝ $\text{[math]}$ (x－1)²＋1

答案解析收藏纠错 + 选题
4. (2022九上·海港月考) 已知x₁、x₂是关于x的一元二次方程x²－(2m＋3)x＋m²＝0的两个不相等的实数根，且满足x₁＋x₂＝m² ，则m的值是（）

A . －1 B . 3 C . 3或－1 D . －3或1

答案解析收藏纠错 + 选题
5. (2018九上·大石桥期末) 如图，将△ABC绕点C顺时针方向旋转40°，得△A′CB′，若AC⊥A′B′，则∠BAC等于（）

A . 50° B . 60° C . 70° D . 80°

答案解析收藏纠错 + 选题
6. (2020九上·房县期中) 二次函数y=a（x+m）²+n的图象如图，则一次函数y=mx+n的图象经过（）

A . 第一、二、三象限 B . 第一、二、四象限 C . 第二、三、四象限 D . 第一、三、四象限

答案解析收藏纠错 + 选题
7. (2022九上·涟水期末) 如图，PA，PB切⊙O于点A，B，点C是⊙O上一点，且∠P＝36°，则∠ACB＝（）

A . 54° B . 72° C . 108° D . 144°

答案解析收藏纠错 + 选题
8. (2018九上·大石桥期末) 在体检中，12名同学的血型结果为：A型3人，B型3人，AB型4人，O型2人，若从这12名同学中随机抽出2人，这两人的血型均为O型的概率为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2018九上·大石桥期末) 如图，△ABC内接于⊙O，AB=BC，∠ABC=120°，AD为⊙O的直径，AD=6，那么AB的值为（）

A . 3 B . $\text{[math]}$ C . 3 $\text{[math]}$ D . 2

答案解析收藏纠错 + 选题
10. (2018九上·大石桥期末) 如图，抛物线y=ax²+bx+c（a≠0）的对称轴为直线x=1，与x轴的一个交点坐标为（-1，0），其部分图象如图所示，下列结论：
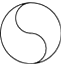
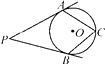
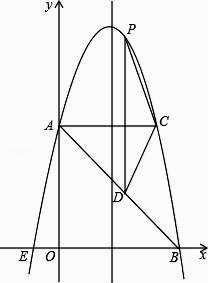
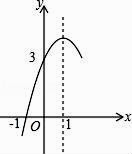
①4ac＜b²；②方程ax²+bx+c=0的两个根是x₁=-1，x₂=3；③3a+c＞0④当y＞0时，x的取值范围是-1≤x＜3⑤当x＜0时，y随x增大而增大其中结论正确的个数是（）

A . 4个 B . 3个 C . 2个 D . 1个

答案解析收藏纠错 + 选题

二、填空题

11. (2018九上·大石桥期末) 点P(－2，5)关于原点对称的点的坐标是．

答案解析收藏纠错 + 选题
12. (2018九上·大石桥期末) 已知抛物线y＝ax²＋bx＋c(a≠0)与x轴的两个交点的坐标分别是(－3，0)，(2，0)，则方程ax²＋bx＋c＝0(a≠0)的解是.

答案解析收藏纠错 + 选题
13. (2018九上·大石桥期末) 从－ $\text{[math]}$ ，0， $\text{[math]}$ ，π，3.5这五个数中，随机抽取一个，则抽到无理数的概率是．

答案解析收藏纠错 + 选题
14. (2018九上·大石桥期末) 已知二次函数y=-x²-2x+3的图象上有两点A（-8，y₁），B（-5，y₂），则y₁y₂ ．（填“＞”“＜”或“=”）

答案解析收藏纠错 + 选题
15. (2018九上·大石桥期末) 已知AB，AC分别是同一圆的内接正方形和内接正六边形的边，那么∠ACB度数为．

答案解析收藏纠错 + 选题
16. (2018九上·大石桥期末) 如图，顺次连接圆内接矩形各边的中点，得到菱形ABCD，若BD＝10，DF＝4，则菱形ABCD的边长为．

答案解析收藏纠错 + 选题
17. (2018九上·大石桥期末) 如图，⊙O的半径为2，点A、C在⊙O上，线段BD经过圆心O，∠ABD=∠CDB=90°，AB=1，CD= $\text{[math]}$ ，则图中阴影部分的面积为．

答案解析收藏纠错 + 选题
18. (2018九上·大石桥期末) 如图，圆心都在x轴正半轴上的半圆O₁ ，半圆O₂ ， …，半圆O_n与直线l相切．设半圆O₁ ，半圆O₂ ， …，半圆O_n的半径分别是r₁ ， r₂ ， …，r_n ，则当直线l与x轴所成锐角为30°，且r₁＝1时，r₂₀₁₈＝.

答案解析收藏纠错 + 选题

三、解答题

19. (2022九上·灞桥开学考) 用适当的方法解下列方程。
1. （1） 3x(x+3)=2(x+3)
2. （2） 2x²−4x−3=0.
答案解析收藏纠错 + 选题
20. (2018九上·大石桥期末) 如图，在平面直角坐标系中，△ABC的三个顶点坐标分别为A（1，4），B（4，2），C（3，5）（每个方格的边长均为1个单位长度）．
1. （1）将△ABC绕点O逆时针旋转90°，画出旋转后得到的△A₁B₁C₁；
2. （2）求出点B旋转到点B₁所经过的路径长．
答案解析收藏纠错 + 选题
21. (2018九上·大石桥期末) 在一个不透明的口袋中装有3个带号码的球，球号分别为2，3，4，这些球除号码不同外其它均相同。甲、乙、两同学玩摸球游戏，游戏规则如下：
先由甲同学从中随机摸出一球，记下球号，并放回搅匀，再由乙同学从中随机摸出一球，记下球号。将甲同学摸出的球号作为一个两位数的十位上的数，乙同学的作为个位上的数。若该两位数能被4整除，则甲胜，否则乙胜.
问：这个游戏公平吗？请说明理由。

答案解析收藏纠错 + 选题
22. (2018九上·大石桥期末) 现代互联网技术的广泛应用，催生了快递行业的高度发展，据调查，长沙市某家小型“大学生自主创业”的快递公司，今年三月份与五月份完成投递的快递总件数分别为10万件和12.1万件，现假定该公司每月投递的快递总件数的增长率相同．
1. （1）求该快递公司投递总件数的月平均增长率；
2. （2）如果平均每人每月最多可投递0.6万件，那么该公司现有的21名快递投递业务员能否完成今年6月份的快递投递任务？如果不能，请问至少需要增加几名业务员？
答案解析收藏纠错 + 选题
23. (2018九上·大石桥期末) 如图，在△ABC中，AB＝AC，以AB为直径的⊙O分别与BC，AC交于点D，E，过点D作DF⊥AC于点F.
1. （1）判断DF与是⊙O的位置关系，并证明你的结论。
2. （2）若⊙O的半径为4，∠CDF＝22.5°，求阴影部分的面积．
答案解析收藏纠错 + 选题
24. (2018九上·大石桥期末) 为了落实国务院的指示精神，政府出台了一系列“三农”优惠政策，使农民收入大幅度增加．某农户生产经销一种农产品，已知这种产品的成本价为每千克20元，市场调查发现，该产品每天的销售量y（千克）与销售价x（元/千克）有如下关系：y=-x+60．设这种产品每天的销售利润为w元．
1. （1）求w与x之间的函数关系式．
2. （2）该产品销售价定为每千克多少元时，每天的销售的最大利润是多少元？
3. （3）如果物价部门规定这种产品的销售价不能高于每千克35元，该农户想要每天获得300元的销售利润，销售价应定为每千克多少元？
答案解析收藏纠错 + 选题
25. (2018九上·大石桥期末) 已知∠AOB＝90°，在∠AOB的平分线OM上有一点C，将一个三角板的直角顶点与C重合，它的两条直角边分别与OA，OB(或它们的反向延长线)相交于点D，E.
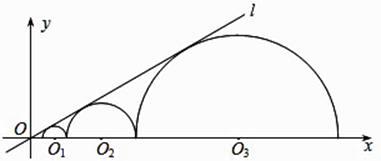
当三角板绕点C旋转到CD与OA垂直时(如图①)，易证：OD＋OE＝ $\text{[math]}$ OC；
当三角板绕点C旋转到CD与OA不垂直时，即在图②，图③这两种情况下，上述结论是否仍然成立？若成立，请给予证明；若不成立，线段OD，OE，OC之间又有怎样的数量关系？请写出你的猜想，不需证明．

答案解析收藏纠错 + 选题
26. (2018九上·大石桥期末) 如图，在平面直角坐标系中，抛物线y=ax²+bx+c的顶点坐标为（2，9），与y轴交于点A（0，5），与x轴交于点E、B．
1. （1）求二次函数y=ax²+bx+c的表达式；
2. （2）过点A作AC平行于x轴，交抛物线于点C，点P为抛物线上的一点（点P在AC上方），作PD平行于y轴交AB于点D，问当点P在何位置时，四边形APCD的面积最大？并求出最大面积；
3. （3）若点M在抛物线上，点N在其对称轴上，使得以A、E、N、M为顶点的四边形是平行四边形，且AE为其一边，求点M、N的坐标．
答案解析收藏纠错 + 选题