 B .
B .  C .
C .  D .
D . 
波长(m) | 300 | 500 | 600 | 1000 | 1500 |
频率(kHz) | 1000 | 600 | 500 | 300 | 200 |
根据表中波长(m)和频率(kHz)的对应关系,当波长为800m时,频率为 kHz.
小亮早晨从家骑车到学校,先上坡后下坡,所行路程y(米)与时间x(分钟)的关系如图所示,若返回时上坡、下坡的速度仍与去时上、下坡的速度分别相同,则小明从学校骑车回家用的时间是分钟.

如图1,是边长为a的大正方形去掉一个边长为b的小正方形形成的,设其阴影部分面积为S1 , 将图1的阴影部分沿虚线剪开拼成的长方形如图2,拼接不重叠且无缝隙,设长方形面积为S2 .

春天来了,小颖要用总长为12米的篱笆围一个长方形花圃,其一边靠墙(墙长9米),另外三边是篱笆,其中BC不超过9米.设垂直于墙的两边AB,CD的长均为x米,长方形花圃的面积为y米2 .

根据关系式补充表格:
x(米) | … | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 | 4.5 | … |
y(米2) | … | 13.5 | 16 | 17.5 | 17.5 | 13.5 | … |
观察表中数据,写出y随x变化的一个特征:.
第1个等式:22﹣12=2×1+1=3;
第2个等式:32﹣22=2×2+1=5;
第3个等式:42﹣32=2×3+1=7;
第4个等式: ;
…
第n个等式: . (n为整数,且n≥1)
A.利用以上规律,计算20012﹣20002的值.
B.利用以上规律,求3+5+7+…+1999的值.
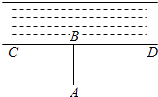
如图1,已知点A是BC外一点,连接AB,AC.
求∠BAC+∠B+∠C的度数.
阅读并补充下面推理过程.
解:过点A作ED∥BC,所以∠B=,∠C=.
又因为∠EAB+∠BAC+∠DAC=180°.
所以∠B+∠BAC+∠C=180°.
从上面的推理过程中,我们发现平行线具有“等角转化”的功能,将∠BAC,∠B,∠C“凑”在一起,得出角之间的关系,使问题得以解决.
方法运用:
如图2,已知AB∥ED,求∠B+∠BCD+∠D的度数.
提示:过点C作CF∥AB.
已知AB∥CD,点C在点D的右侧,∠ADC=70°,BE平分∠ABC,DE平分∠ADC,BE,DE所在的直线交于点E,点E在AB与CD两条平行线之间.
请从下面的A,B两题中任选一题解答.
A.如图3,点B在点A的左侧,若∠ABC=60°,则∠BED的度数为°.
B.如图4,点B在点A的右侧,且AB<CD,AD<BC.若∠ABC=n°,则∠BED的度数为°.(用含n的代数式表示)