浙江省嘉兴市海宁新仓中学2019届九年级上学期数学第一次月考...

更新时间：2018-11-26 浏览次数：468 类型：月考试卷

一、单选题

1. (2022九上·邯郸冀南新期中) 若二次函数y=x²﹣2x+c的图象与x轴没有交点，则c的值可能是（）

A . ﹣3 B . ﹣2 C . 0 D . 2

答案解析收藏纠错 + 选题
2. (2018九上·嘉兴月考) 方程ax²+bx+c=0的两个根是-3和1，那么二次函数y=ax²+bx+c的图象的对称轴是直线（）

A . x＝-3 B . x＝-2 C . x＝-1 D . x＝1

答案解析收藏纠错 + 选题
3. (2020九上·绍兴月考) 下列说法中错误的是（）

A . 某种彩票的中奖率为1%，买100张彩票一定有1张中奖 B . 从装有10个红球的袋子中，摸出1个白球是不可能事件 C . 为了解一批日光灯的使用寿命，可采用抽样调查的方式 D . 掷一枚普通的正六面体骰子，出现向上一面点数是2的概率是 $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2018九上·嘉兴月考) 抛物线y=2（x﹣3）²+1的顶点坐标是（）

A . （3，1） B . （3，﹣1） C . （﹣3，1） D . （﹣3，﹣1）

答案解析收藏纠错 + 选题
5. (2018九上·嘉兴月考) 在不透明的布袋中装有2个白球，3个黑球，它们除颜色外完全相同，从袋中任意摸出一个球，摸出的球是白球的概率是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2018九上·嘉兴月考) 二次函数y=﹣x²+2x的图象可能是（）

A . B . C . D .

答案解析收藏纠错 + 选题
7. (2018九上·嘉兴月考) 如图，已知二次函数 $\text{[math]}$ 的图象与正比例函数 $\text{[math]}$ 的图象交于点A（3，2），与x轴交于点B（2，0），若0＜y₁＜y₂ ，则x的取值范围是（）

A . 0＜x＜2 B . 0＜x＜3 C . 2＜x＜3 D . x＜0或x＞3

答案解析收藏纠错 + 选题
8. (2023九上·柯桥月考) 在同一坐标系中，函数y=ax²与y=ax+a（a＜0）的图象的大致位置可能是（　　）

A . B . C . D .

答案解析收藏纠错 + 选题
9. (2018九上·嘉兴月考) 二次函数y=ax²+bx+c (a、b、c为常数且a≠0)中的x与y的部分对应值如下表，
x
…
-3
-2
-1
0
1
2
3
4
5
…
y
…
12
5
0
-3
-4
-3
0
5
12
…
下列四个结论：
①二次函数y=ax²+bx+c 有最小值，最小值为-3；②抛物线与y轴交点为（0，-3）；③二次函数y=ax²+bx+c 的图像对称轴是x=1；④本题条件下，一元二次方程ax²+bx+c=0的解是x₁=-1，x₂=3.其中正确结论的个数是（）

A . 4 B . 3 C . 2 D . 1

答案解析收藏纠错 + 选题
10. (2018九上·嘉兴月考) 已知二次函数y=ax²+bx+c（a≠0）的图象如图，且关于x的一元二次方程ax²+bx+c﹣m=0没有实数根，有下列结论：①b²﹣4ac＞0；②abc＜0；③m＞2．其中，正确结论的个数是（）.

A . 0 B . 1 C . 2 D . 3

答案解析收藏纠错 + 选题

二、填空题

11. (2018九上·嘉兴月考) 将抛物线 $\text{[math]}$ 平移，使它的顶点移到点P（-2，3），平移后新抛物线的表达式为．

答案解析收藏纠错 + 选题
12. (2018九上·嘉兴月考) 一根长为100cm的铁丝围成一个矩形框，要想使铁丝框的面积最大，边长分别为．

答案解析收藏纠错 + 选题
13. (2018九上·嘉兴月考) 在一个不透明的盒子中装有n个规格相同的乒乓球，其中有2个黄色球，每次摸球前先将盒中的球摇匀，随机摸出一个球记下颜色后再放回盒中，通过大量重复试验后发现，摸到黄色球的频率稳定于0.2，那么可以推算出n大约是．

答案解析收藏纠错 + 选题
14. (2023·青浦模拟) 将抛物线y=x²向左平移1个单位后的抛物线表达式为．

答案解析收藏纠错 + 选题
15. (2018九上·嘉兴月考) 已知二次函数y=x²+（m﹣1）x+1，当x＞1时，y随x的增大而增大，则m的取值范围是．

答案解析收藏纠错 + 选题
16. (2018九上·嘉兴月考) 在一个不透明的袋子里装有黄色、白色乒乓球共40个，除颜色外其他完全相同．从这个袋子中随机摸出一球，放回．通过多次摸球实验后发现，摸到黄色球的概率稳定在15%附近，则袋中黄色球可能有个．

答案解析收藏纠错 + 选题
17. (2018九上·嘉兴月考) 已知关于x的方程（a+2）x²﹣2ax+a=0有两个不相等的实数根x₁和x₂ ，抛物线y=x²﹣（2a+1）x+2a﹣5与x轴的两个交点分别为位于点（2，0）的两旁，若|x₁|+|x₂|=2 $\text{[math]}$ ，则a的值为．

答案解析收藏纠错 + 选题
18. (2018九上·嘉兴月考) 在平面直角坐标系xOy中，将抛物线 $\text{[math]}$ 平移后得到抛物线 $\text{[math]}$ .请你写出一种平移方法. 答：.

答案解析收藏纠错 + 选题

三、解答题

19. (2018九上·嘉兴月考) 如图，在△ABC中，∠B=90°，AB=12，BC=24，动点P从点A开始沿边AB向终点B以每秒2个单位长度的速度移动，动点Q从点B开始沿边BC以每秒4个单位长度的速度向终点C移动，如果点P、Q分别从点A、B同时出发，那么△PBQ的面积S随出发时间t（s）如何变化？写出函数关系式及t的取值范围．

答案解析收藏纠错 + 选题
20. (2018九上·嘉兴月考) 某商店购进一批单价为20元的日用品，如果以单价30元销售，那么半个月内可以售出400件.根据销售经验，提高销售单价会导致销售量的减少，即销售单价每提高1元，销售量相应减少20件.问如何提高售价，才能在半个月内获得最大利润？

答案解析收藏纠错 + 选题
21. (2018九上·嘉兴月考) 在2014年“元旦”前夕，某商场试销一种成本为30元的文化衫，经试销发现，若每件按34元的价格销售，每天能卖出36件；若每件按39元的价格销售，每天能卖出21件．假定每天销售件数y（件）是销售价格x(元)的一次函数．
1. （1）直接写出y与x之间的函数关系式.
2. （2）在不积压且不考虑其他因素的情况下，每件的销售价格定为多少元时，才能使每天获得的利润P最大？
答案解析收藏纠错 + 选题
22. (2018九上·嘉兴月考) 若函数y=（a-1）x^（^b+1^）+x²+1是二次函数，试讨论a、b的取值范围.

答案解析收藏纠错 + 选题
23. (2018九上·嘉兴月考) 如图，抛物线y=ax²+bx+c过原点O、点A （2，﹣4）、点B （3，﹣3），与x轴交于点C，直线AB交x轴于点D，交y轴于点E．
1. （1）求抛物线的函数表达式和顶点坐标；
2. （2）直线AF⊥x轴，垂足为点F，AF上取一点G，使△GBA∽△AOD，求此时点G的坐标；
3. （3）过直线AF左侧的抛物线上点M作直线AB的垂线，垂足为点N，若∠BMN=∠OAF，求直线BM的函数表达式．
答案解析收藏纠错 + 选题
24. (2019九上·洛阳月考) 已知：如图，抛物线y=﹣x²+bx+c与x轴交于点A（﹣1，0），B（3，0），与y轴交于点C．过点C作CD∥x轴，交抛物线的对称轴于点D．
1. （1）求该抛物线的解析式；
2. （2）若将该抛物线向下平移m个单位，使其顶点落在D点，求m的值．
答案解析收藏纠错 + 选题
25. (2018九上·嘉兴月考) 如图所示，在平面直角坐标系xOy中，正方形OABC的边长为2cm，点A、C分别在y轴的负半轴和x轴的正半轴上，抛物线 $\text{[math]}$ 经过点A、B和D（4， $\text{[math]}$ ）．
1. （1）求抛物线的表达式．
2. （2）如果点P由点A出发沿AB边以2cm/s的速度向点B运动，同时点Q由点B出发，沿BC边以1cm/s的速度向点C运动，当其中一点到达终点时，另一点也随之停止运动．设S=PQ²（cm²）．
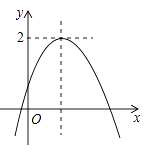
  ①试求出S与运动时间t之间的函数关系式，并写出t的取值范围；
  ②当S取 $\text{[math]}$ 时，在抛物线上是否存在点R，使得以点P、B、Q、R为顶点的四边形是平行四边形?如果存在，求出R点的坐标；如果不存在，请说明理由．
3. （3）在抛物线的对称轴上求点M，使得M到D、A的距离之差最大，求出点M的坐标．
答案解析收藏纠错 + 选题
26. (2018九上·嘉兴月考) 如图，在Rt△ABC中，∠C=90°，顶点A、C的坐标分别为（﹣1，2），（3，2），点B在x轴上，点B的坐标为（3，0），抛物线y=﹣x²+bx+c经过A、C两点．
1. （1）求该抛物线所对应的函数关系式；
2. （2）点P是抛物线上的一点，当S_△_PAB= $\text{[math]}$ S_△_ABC时，求点P的坐标；
3. （3）若点N由点B出发，以每秒 $\text{[math]}$ 个单位的速度沿边BC、CA向点A移动， $\text{[math]}$ 秒后，点M也由点B出发，以每秒1个单位的速度沿线段BO向点O移动，当其中一个点到达终点时另一个点也停止移动，点N的移动时间为t秒，当MN⊥AB时，请直接写出t的值，不必写出解答过程．
答案解析收藏纠错 + 选题