浙江省绍兴市锡麟中学、马山中学等校2021届九年级上学期数学...

更新时间：2021-02-22 浏览次数：123 类型：月考试卷

一、单选题

1. (2023九上·义乌月考) 若 $\text{[math]}$ ，则 $\text{[math]}$ =（）

A . 2 B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2020九上·绍兴月考) 将抛物线 $\text{[math]}$ 向左平移2个单位后，得到的抛物线的解析式是（）.

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2020九上·绍兴月考) 下列说法中错误的是（）

A . 某种彩票的中奖率为1%，买100张彩票一定有1张中奖 B . 从装有10个红球的袋子中，摸出1个白球是不可能事件 C . 为了解一批日光灯的使用寿命，可采用抽样调查的方式 D . 掷一枚普通的正六面体骰子，出现向上一面点数是2的概率是 $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2022九上·西湖期中) 已知（﹣1，y₁），（﹣2，y₂），（﹣4，y₃）是抛物线y=﹣2x²﹣8x+m上的点，则（　　）

A . y₁＜y₂＜y₃ B . y₃＜y₂＜y₁ C . y₃＜y₁＜y₂ D . y₂＜y₃＜y₁

答案解析收藏纠错 + 选题
5. (2020九上·绍兴月考) 如图，AB，CD都垂直于x轴，垂足分别为B，D，若A（6，3），C（2，1），则三角形OCD与四边形ABCD的面积比为（）

A . 1：2 B . 1：3 C . 1：4 D . 1：8

答案解析收藏纠错 + 选题
6. (2020九上·绍兴月考)
如图，二次函数y=a $\text{[math]}$ +bx+c的图象开口向上，对称轴为直线x=1，图象经过（3，0），下列结论中，正确的一项是( )

A . abc＜0 B . 2a＋b＜0 C . a－b＋c＜0 D . 4ac－b²＜0

答案解析收藏纠错 + 选题
7. (2022·沭阳模拟) 如图所示，在平行四边形ABCD中，AC与BD相交于点O，E为OD的中点，连接AE并延长交DC于点F，则DF：FC=（）

A . 1：3 B . 1：4 C . 2：3 D . 1：2

答案解析收藏纠错 + 选题
8. (2020九上·绍兴月考) 如图，A，B，C三点在已知的圆上，在△ABC中，∠ABC=70°，∠ACB=30°，D是 $\text{[math]}$ 的中点，连接DB，DC，则∠DBC的度数为（）

A . 30° B . 45° C . 50° D . 70°

答案解析收藏纠错 + 选题
9. (2021九上·上城期中) 下列语句中，正确的是（）
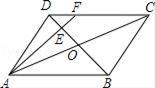
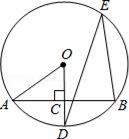
①三个点确定一个圆；②同弧或等弧所对的圆周角相等；③平分弦的直径垂直于弦，并且平分弦所对的弧；④圆内接平行四边形一定是矩形．

A . ①② B . ②③ C . ②④ D . ④

答案解析收藏纠错 + 选题
10. (2020九上·绍兴月考) 在 $\text{[math]}$ 中，点 $\text{[math]}$ 在 $\text{[math]}$ 上，点 $\text{[math]}$ 在 $\text{[math]}$ 上，且 $\text{[math]}$ 与 $\text{[math]}$ 相似， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的长为（）

A . $\text{[math]}$ B . 12 C . $\text{[math]}$ D . $\text{[math]}$ 或 $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题

11. (2021九上·西湖期末) 已知线段a=3，b=27，则线段a、b的比例中项为．

答案解析收藏纠错 + 选题
12. (2020九上·绍兴月考) 如图，已知点C是 $\text{[math]}$ 的一点，圆周角∠ACB为125°，则圆心角∠AOB=度.

答案解析收藏纠错 + 选题
13. (2020九上·绍兴月考) 二次函数y=ax²−3ax+2(a<0)的图象如图所示，若y<2，则x的取值范围为.

答案解析收藏纠错 + 选题
14. (2020九上·绍兴月考) 如图，P是△ABC的重心，过点P作PE∥AB交BC于点E，PF∥AC交BC于点F，若△PEF的周长是6，则△ABC的周长为.

答案解析收藏纠错 + 选题
15. (2020九上·绍兴月考) 如图，点O是半径为3的圆形纸片的圆心，将这个圆形纸片按下列顺序折叠，使 $\text{[math]}$ 和 $\text{[math]}$ 都经过圆心O，则阴影部分面积是。

答案解析收藏纠错 + 选题
16. (2020九上·绍兴月考) 如图，平行于x轴的直线AC分别交抛物线y₁=x²（x≥0）与y₂= $\text{[math]}$ （x≥0）于B、C两点，过点C作y轴的平行线交y₁于点D，直线DE∥AC，交y₂于点E，则 $\text{[math]}$ =．

答案解析收藏纠错 + 选题

三、解答题

17. (2023九上·义乌月考) 如图，D是△ABC的边AC上的一点，连接BD，已知∠ABD=∠C.
1. （1）求证：△ABD∽△ACB
2. （2）若AB=6，AD=4，求线段CD的长
答案解析收藏纠错 + 选题
18. (2021九上·滨海月考) 如图所示，AB是⊙O的一条弦，OD⊥AB，垂足为C，交⊙O于点D，点E在⊙O上．
1. （1）若∠AOD=52°，求∠DEB的度数；
2. （2）若OC=3，OA=5，求AB的长．
答案解析收藏纠错 + 选题
19. (2020九上·绍兴月考) 如图，我们把一个半圆与抛物线的一部分围成的封闭图形称为“果圆”.已知点A、B、C、D分别是“果圆”与坐标轴的交点，抛物线的解析式为y=(x-1)²-4，AB为半圆的直径，求这个“果圆”被y轴截得的CD的长.

答案解析收藏纠错 + 选题
20. (2023九上·柯桥月考)
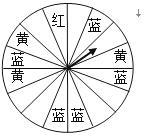
某商场设定了一个可以自由转动的转盘（转盘被等分成16个扇形），并规定：顾客在商场消费每满200元，就能获得一次转动转盘的机会．如果转盘停止后，指针正好对准红、黄和蓝色区域，顾客就可以分别获得50元、30元和10元的购物券．如果顾客不愿意转转盘，则可以直接获得购物券15元．
1. （1）转动一次转盘，获得50元、30元、10元购物券的概率分别是多少？
2. （2）如果有一名顾客在商场消费了200元，通过计算说明转转盘和直接获得购物券，哪种方式对这位顾客更合算？
答案解析收藏纠错 + 选题
21. (2020九上·绍兴月考) 某农场拟建三间矩形饲养室，饲养室一面靠墙（墙可用长≤20m），中间用两道墙隔开，已知计划中的建筑材料可建围墙的总长为60m，设饲养室宽为x（m），总占地面积为y（m²）（如图所示）.
1. （1）求y关于x的函数表达式，并直接写出自变量x的取值范围；
2. （2）三间饲养室占地总面积有可能达到210m²吗？请说明理由.
答案解析收藏纠错 + 选题
22. (2020九上·绍兴月考) 如图，在Rt△ABC中，∠BAC=90°，AB=6，AC=8，点D为边BC的中点，点P为射线AB上的一动点，点Q为边AC上的一动点，且∠PDQ=90°.
1. （1）当DP⊥AB时，求CQ的长；
2. （2）当BP=2，求CQ的长
答案解析收藏纠错 + 选题
23. (2020九上·绍兴月考) 已知一次函数y=− $\text{[math]}$ x−12的图象分别交x轴，y轴于A，C两点。
1. （1）求出A，C两点的坐标；
2. （2）在x轴上找出点B，使△ACB∽△AOC，若抛物线过A，B，C三点，求出此抛物线的解析式；
3. （3）在(2)的条件下，设动点P、Q分别从A，B两点同时出发，以相同速度沿AC、BA向C，A运动，连接PQ，设AP=m，是否存在m值，使以A，P，Q为顶点的三角形与△ABC相似?若存在，求出所有m值；若不存在，请说明理由。
答案解析收藏纠错 + 选题
24. (2020九上·绍兴月考) 在平面直角坐标系 $\text{[math]}$ 中，规定：抛物线 $\text{[math]}$ 的伴随直线为 $\text{[math]}$ .例如：抛物线 $\text{[math]}$ 的伴随直线为 $\text{[math]}$ ，即 $\text{[math]}$
1. （1）在上面规定下，抛物线 $\text{[math]}$ 的顶点为.伴随直线为；
2. （2）若顶点在第一象限的抛物线 $\text{[math]}$ 与其伴随直线相交于点A，B (点A在点B的左侧)，抛物线与x轴交于点C、D(点C在点D的左侧).
  ①若 $\text{[math]}$ 求m的值；
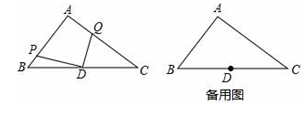
  ②如果点 $\text{[math]}$ 是直线BC上方抛物线的一个动点， $\text{[math]}$ 的面积记为S，当S取得最大值 $\text{[math]}$ 时，求m的值.
答案解析收藏纠错 + 选题