2016-2017学年广东省深圳市罗湖区九年级上学期期末数学...

更新时间：2017-03-28 浏览次数：487 类型：期末考试

一、选择题：

1. (2017九上·罗湖期末) 一元二次方程x²﹣1=0的根为（）

A . x=1 B . x=﹣1 C . x₁=1，x₂=﹣1 D . x₁=0，x₂=1

答案解析收藏纠错 + 选题
2. (2017九上·罗湖期末) 在Rt△ABC中，∠C=90°，AC=3，BC=4，那么cosB的值是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2023·周村模拟) 有一个铁制零件（正方体中间挖去一个圆柱形孔）如图放置，它的左视图是（）

A . B . C . D .

答案解析收藏纠错 + 选题
4. (2017九上·罗湖期末) 下列命题正确的是（）

A . 有一组邻边相等的四边形是菱形 B . 有一个角是直角的平行四边形是矩形 C . 对角线互相垂直的平行四边形是正方形 D . 对角线相等且互相垂直的四边形是正方形

答案解析收藏纠错 + 选题
5. (2017九上·罗湖期末) 如图，小明从路灯下A处向前走了5米，发现自己在地面上的影子长DE是2米，如果小明的身高为1.6米，那么路灯离地面的高度AB是（）

A . 4米 B . 5.6米 C . 2.2米 D . 12.5米

答案解析收藏纠错 + 选题
6. (2017九上·罗湖期末) 已知二次函数y=ax²的图象如图所示，则关于x的一元二次方程x²+x+a﹣1=0的根的存在情况是（）

A . 没有实数根 B . 有两个相等的实数根 C . 有两个不相等的实数根 D . 无法确定

答案解析收藏纠错 + 选题
7. (2024九上·武汉月考) 某公司今年销售一种产品，一月份获得利润10万元，由于产品畅销，利润逐月增加，一季度共获利36.4万元，已知2月份和3月份利润的月增长率相同．设2，3月份利润的月增长率为x，那么x满足的方程为（）

A . 10（1+x）²=36.4 B . 10+10（1+x）²=36.4 C . 10+10（1+x）+10（1+2x）=36.4 D . 10+10（1+x）+10（1+x）²=36.4

答案解析收藏纠错 + 选题
8. (2019九上·淮南月考) 已知等腰三角形的腰和底的长分别是一元二次方程x²﹣4x+3=0的根，则该三角形的周长可以是（）

A . 5 B . 7 C . 5或7 D . 10

答案解析收藏纠错 + 选题
9. (2017八下·长春期末) 如图，延长矩形ABCD的边BC至点E，使CE=BD，连结AE，如果∠ADB=30°，则∠E的度数是（）

A . 45° B . 30° C . 20° D . 15°

答案解析收藏纠错 + 选题
10. (2017九上·罗湖期末) 如图是二次函数y=ax²+bx+c图象的一部分，图象过点A（﹣3，0），对称轴为x=﹣1．给出四个结论：①b²＞4ac；②2a+b=0；③a﹣b+c=0；④5a＜b．其中正确结论是（）

A . ②④ B . ①④ C . ②③ D . ①③

答案解析收藏纠错 + 选题
11. (2017九上·罗湖期末) 如图，在菱形ABCD中，∠BAD=60°，点M是AB的中点，P是对角线AC上的一个动点，若PM+PB的最小值是9，则AB的长是（）

A . 6 $\text{[math]}$ B . 3 $\text{[math]}$ C . 9 D . 4.5

答案解析收藏纠错 + 选题
12. (2017九上·罗湖期末) 如图，已知直线y= $\text{[math]}$ x与双曲线y= $\text{[math]}$ （k＞0）交于A、B两点，点B的坐标为（﹣4，﹣2），C为双曲线y= $\text{[math]}$ （k＞0）上一点，且在第一象限内，若△AOC的面积为6，则点C的坐标为（）

A . （2，4） B . （1，8） C . （2，4）或（1，8） D . （2，4）或（8，1）

答案解析收藏纠错 + 选题

二、填空题：

13. (2017九上·罗湖期末) 某口袋中有红色、黄色、蓝色玻璃球共72个，小明通过多次摸球试验后，发现摸到红球、黄球、蓝球的频率为35%、25%和40%，估计口袋中黄色玻璃球有个．

答案解析收藏纠错 + 选题
14. (2017九上·罗湖期末) 若关于x的一元二次方程（m﹣1）x²+5x+m²﹣3m+2=0的一个根是0，则m的值是．

答案解析收藏纠错 + 选题
15. (2017九上·罗湖期末)
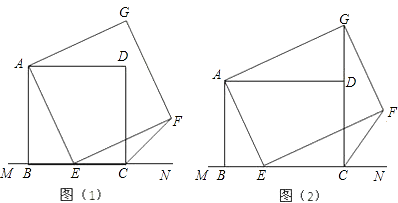
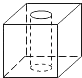
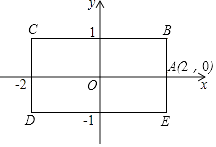
如图，矩形BCDE的各边分别平行于x轴或y轴，物体甲和物体乙分别由点A（2，0）同时出发，沿矩形BCDE的边作环绕运动，物体甲按逆时针方向以1个单位/秒匀速运动，物体乙按顺时针方向以2个单位/秒匀速运动，则两个物体运动后的第2016次相遇地点的坐标是．

答案解析收藏纠错 + 选题
16. (2017九上·罗湖期末) 如图1，在矩形纸片ABCD中，AB=8 $\text{[math]}$ ，AD=10，点E是CD中点，将这张纸片依次折叠两次；第一次折叠纸片使点A与点E重合，如图2，折痕为MN，连接ME、NE；第二次折叠纸片使点N与点E重合，如图3，点B落到B′处，折痕为HG，连接HE，则tan∠EHG=．

答案解析收藏纠错 + 选题

三、解答题：

17. (2017九上·罗湖期末) 解方程：
1. （1） x²+3x﹣2=0；
2. （2）（x﹣3）（x+1）=x﹣3．
答案解析收藏纠错 + 选题
18. (2017九上·罗湖期末) 小明参加某网店的“翻牌抽奖”活动，如图，4张牌分别对应价值5，10，15，20（单位：元）的4件奖品．
1. （1）如果随机翻1张牌，那么抽中20元奖品的概率为．
2. （2）如果随机翻2张牌，且第一次翻过的牌不再参加下次翻牌，请用列表或画树状图的方法求出所获奖品总值不低于30元的概率为多少？
答案解析收藏纠错 + 选题
19. (2017九上·罗湖期末) 如图．矩形ABCD的对角线相交于点O．DE∥AC，CE∥BD．
1. （1）求证：四边形OCED是菱形；
2. （2）若∠ACB=30°，菱形OCED的面积为8 $\text{[math]}$ ，求AC的长．
答案解析收藏纠错 + 选题
20. (2022·成都模拟)
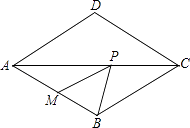
如图，在两建筑物之间有一旗杆，高15米，从A点经过旗杆顶点恰好看到矮建筑物的墙角C点，且俯角α为60°，又从A点测得D点的俯角β为30°，若旗杆底部G点为BC的中点，求矮建筑物的高CD．

答案解析收藏纠错 + 选题
21. (2017九上·罗湖期末) 某景区商店购进600个旅游纪念品，进价为每个6元，第一周以每个10元的价格售出200个；第二周若按每个10元的价格销售仍可售出200个，但商店为了提高销售量，决定降价销售（根据市场调查，单价每降低1元，可多售出50个，但售价不得低于进价），单价降低x元销售一周后，商店对剩余旅游纪念品清仓处理，以每个4元的价格全部售出．
1. （1）如果这批旅游纪念品共获利1050元，那么第二周每个旅游纪念品的销售价格为多少元？
2. （2）第二周每个旅游纪念品的销售价格为多少时，这批旅游纪念品利润最大？最大利润是多少？
答案解析收藏纠错 + 选题
22. (2017九上·罗湖期末) 如图（1），已知正方形ABCD在直线MN的上方，BC在直线MN上，E是BC上一点，以AE为边在直线MN的上方作正方形AEFG．
1. （1）连接GD，求证：△ADG≌△ABE；
2. （2）连接FC，观察并猜测∠FCN的度数，并说明理由；
3. （3）如图（2），将图（1）中正方形ABCD改为矩形ABCD，AB=a，BC=b（a、b为常数），E是线段BC上一动点（不含端点B、C），以AE为边在直线MN的上方作矩形AEFG，使顶点G恰好落在射线CD上．判断当点E由B向C运动时，∠FCN的大小是否总保持不变？若∠FCN的大小不变，请用含a、b的代数式表示tan∠FCN的值；若∠FCN的大小发生改变，请举例说明．
答案解析收藏纠错 + 选题
23. (2017九上·罗湖期末)
如图，抛物线y=ax²+bx+c经过△ABC的三个顶点，与y轴相交于（0， $\text{[math]}$ ），点A坐标为（﹣1，2），点B是点A关于y轴的对称点，点C在x轴的正半轴上．
1. （1）求该抛物线的函数关系表达式．
2. （2）点F为线段AC上一动点，过F作FE⊥x轴，FG⊥y轴，垂足分别为E、G，当四边形OEFG为正方形时，求出F点的坐标．
3. （3）将（2）中的正方形OEFG沿OC向右平移，记平移中的正方形OEFG为正方形DEFG，当点E和点C重合时停止运动，设平移的距离为t，正方形的边EF与AC交于点M，DG所在的直线与AC交于点N，连接DM，是否存在这样的t，使△DMN是等腰三角形？若存在，求t的值；若不存在请说明理由．
答案解析收藏纠错 + 选题