安徽省淮南市西部地区2019-2020学年九年级上学期数学1...

更新时间：2020-08-25 浏览次数：220 类型：月考试卷

一、单选题

1. (2019九上·淮南月考) 下列方程中，一定是关于x的一元二次方程的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2019九上·淮南月考) 若1﹣ $\text{[math]}$ 是方程x²﹣2x+c=0的一个根，则c的值为（）

A . ﹣2 B . 4 $\text{[math]}$ ﹣2 C . 3﹣ $\text{[math]}$ D . 1+ $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2019九上·淮南月考) 若 $\text{[math]}$ 是二次函数，则m的值为（）

A . 2 B . -1 C . -1或2 D . 以上都不对

答案解析收藏纠错 + 选题
4. (2019九上·淮南月考) 方程 $\text{[math]}$ 的二次项系数、一次项系数、常数项分别为（）

A . 6，2，9 B . 2，－6，9 C . －2，－6，9 D . 2，－6，－9

答案解析收藏纠错 + 选题
5. (2019九上·淮南月考) 二次函数y＝ax²+bx+c的图象如图所示，根据图象可得a ， b ， c与0的大小关系是（）

A . a＞0，b＜0，c＜0 B . a＞0，b＞0，c＞0 C . a＜0，b＜0，c＜0 D . a＜0，b＞0，c＜0

答案解析收藏纠错 + 选题
6. (2019九上·淮南月考) 已知等腰三角形的腰和底的长分别是一元二次方程x²﹣4x+3=0的根，则该三角形的周长可以是（）

A . 5 B . 7 C . 5或7 D . 10

答案解析收藏纠错 + 选题
7. (2023九上·汶上月考) 某品牌网上专卖店1月份的营业额为50万元，已知第一季度的总营业额共600万元，如果平均每月增长率为x ，则由题意列方程应为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2020九上·莲池期中) 若关于x的一元二次方程（k﹣1）x²+2x﹣2=0有两个不相等的实数根，则k的取值范围是（）

A . k＞ $\text{[math]}$ B . k≥ $\text{[math]}$ C . k＞ $\text{[math]}$ 且k≠1 D . k≥ $\text{[math]}$ 且k≠1

答案解析收藏纠错 + 选题
9. (2023九上·长沙月考) 已知函数 $\text{[math]}$ 的图象如图，那么关于x的方程 $\text{[math]}$ 的根的情况是 $\text{[math]}$ $\text{[math]}$

A . 无实数根 B . 有两个相等实数根 C . 有两个同号不等实数根 D . 有两个异号实数根

答案解析收藏纠错 + 选题
10. (2020九上·孝感月考) 在平面直角坐标系xOy中，开口向下的抛物线y＝ax²＋bx＋c的一部分图象如图所示，它与x轴交于A(1，0)，与y轴交于点B(0，3)，则a的取值范围是（）

A . a＜0 B . －3＜a＜0 C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题

11. (2019九上·淮南月考) 一元二次方程的两根是0，2，则这个一元二次方程为.

答案解析收藏纠错 + 选题
12. (2019九上·淮南月考) 若点A（1，y₁），B（2，y₂）在抛物线y＝﹣ $\text{[math]}$ （x+1）²﹣1上，则y₁ y₂ ．

答案解析收藏纠错 + 选题
13. (2019九上·淮南月考) 抛物线 $\text{[math]}$ 的部分图象如图所示，对称轴是直线 $\text{[math]}$ ，则关于x的一元二次方程 $\text{[math]}$ 的解为．

答案解析收藏纠错 + 选题
14. (2019九上·淮南月考) 已知关于x的二次函数y₁＝x²﹣2x与一次函数y₂＝x+4，若y₁＞y₂ ，则x的取值范围是．

答案解析收藏纠错 + 选题

三、解答题

15. (2019九上·淮南月考) 解方程： $\text{[math]}$ .

答案解析收藏纠错 + 选题
16. (2019九上·淮南月考) 若二次函数y=x²+bx+c的图象经过点（0，1）和（1，﹣2）两点，求此二次函数的表达式．

答案解析收藏纠错 + 选题
17. (2019九上·西城期中) 已知二次函数 $\text{[math]}$ .
1. （1）用配方法将二次函数的表达式化为 $\text{[math]}$ 的形式；
2. （2）在平面直角坐标系 $\text{[math]}$ 中，画出这个二次函数的图象；
3. （3）根据（2）中的图象，写出一条该二次函数的性质.
答案解析收藏纠错 + 选题
18. (2019九上·武城期中) 已知关于x的方程 $\text{[math]}$
1. （1）求证：方程总有两个实数根
2. （2）若方程有一个小于1的正根，求实数k的取值范围
答案解析收藏纠错 + 选题
19. (2019九上·淮南月考) 某水果店销售一种水果的成本价是5元/千克．在销售过程中发现，当这种水果的价格定在7元/千克时，每天可以卖出160千克．在此基础上，这种水果的单价每提高1元/千克，该水果店每天就会少卖出20千克．
1. （1）若该水果店每天销售这种水果所获得的利润是420元，则单价应定为多少？
2. （2）在利润不变的情况下，为了让利于顾客，单价应定为多少？
答案解析收藏纠错 + 选题
20. (2019九上·淮南月考) “a²=0”这个结论在数学中非常有用，有时我们需要将代数式配成完全平方式，例如：x²+4x+5=x²+4x+4+1=（x+2）²+1，∵（x+2）²≥0，（x+2）2+1≥1，∴x²+4x+5≥1．试利用“配方法”解决下列问题：
1. （1）填空：因为x²﹣4x+6=（x）²+；所以当x=时，代数式x²﹣4x+6有最（填“大”或“小”）值，这个最值为．
2. （2）比较代数式x²﹣1与2x﹣3的大小．
答案解析收藏纠错 + 选题
21. (2019九上·淮南月考) 下列图形都是由同样大小的菱形按照一定规律组成的，请根据排列规律完成下列问题：
1. （1）填写下表：
  
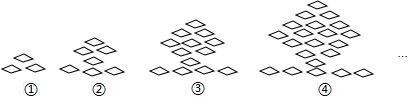
  图形序号
  
  菱形个数 $\text{[math]}$ 个 $\text{[math]}$
  
  $\text{[math]}$
  
  3
  
  $\text{[math]}$
  
  7
  
  $\text{[math]}$
  
  $\text{[math]}$
  
  $\text{[math]}$
  
  $\text{[math]}$
2. （2）根据表中规律猜想，图n中菱形的个数 $\text{[math]}$ 用含n的式子表示，不用说理 $\text{[math]}$ ；
3. （3）是否存在一个图形恰好由91个菱形组成？若存在，求出图形的序号；若不存在，说明理由.
答案解析收藏纠错 + 选题
22. (2019九上·淮南月考) 已知关于x的一元二次方程 $\text{[math]}$ 有实数根．
1. （1）求m的值；
2. （2）先作 $\text{[math]}$ 的图象关于x轴的对称图形，然后将所作图形向左平移3个单位长度，再向上平移2个单位长度，写出变化后图象的解析式；
3. （3）在（2）的条件下，当直线y=2x+n（n≥m）与变化后的图象有公共点时，求 $\text{[math]}$ 的最大值和最小值．
答案解析收藏纠错 + 选题

23. (2019九上·淮南月考) 阅读下列材料：有这样一个问题：关于x的一元二次方程 $\text{[math]}$ 有两个不相等的且非零的实数根探究a，b，c满足的条件.

小明根据学习函数的经验，认为可以从二次函数的角度看一元二次方程，下面是小明的探究过程：①设一元二次方程 $\text{[math]}$ 对应的二次函数为 $\text{[math]}$ ；

②借助二次函数图象，可以得到相应的一元二次中a，b，c满足的条件，列表如下：

（1）参考小明的做法，把表格补充完整；

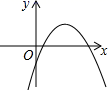
方程根的几何意义：

方程两根的情况	对应的二次函数的大致图象	a，b，c满足的条件
方程有两个不相等的负实根		$\text{[math]}$
		$\text{[math]}$
方程有两个不相等的正实根

（2）若一元二次方程 $\text{[math]}$ 有一个负实根，一个正实根，且负实根大于-1，求实数m的取值范围.

答案解析收藏纠错 + 选题

试卷信息

小学

初中

高中

安徽省淮南市西部地区2019-2020学年九年级上学期数学1...

副标题：

*注意事项：

安徽省淮南市西部地区2019-2020学年九年级上学期数学1...

试题分析

总体分析

题量分析

难度分析

知识点分析

图形序号	菱形个数 $\text{[math]}$ 个 $\text{[math]}$
$\text{[math]}$	3
$\text{[math]}$	7
$\text{[math]}$
$\text{[math]}$
$\text{[math]}$	$\text{[math]}$