2016-2017学年江西省宜春市九年级上学期期末数学试卷

更新时间：2017-04-18 浏览次数：1162 类型：期末考试

一、选择题

1. (2017九上·宜春期末) 下列图形中，是中心对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
2. 抛物线y=（x﹣2016）²+2017的顶点坐标是（）

A . （2016，﹣2017） B . （﹣2016，2017） C . （2016，2017） D . （﹣2016，﹣2017）

答案解析收藏纠错 + 选题
3. (2016九上·仙游期中) 下列诗句所描述的事件中，是不可能事件的是（）

A . 黄河入海流 B . 锄禾日当午 C . 大漠孤烟直 D . 手可摘星辰

答案解析收藏纠错 + 选题
4. (2017九上·宜春期末) 要做一顶母线长为20cm，底面半径为10cm的纸质圆锥形圣诞帽，至少需要纸的面积为（）

A . 300πcm² B . 250πcm² C . 200πcm² D . 150πcm²

答案解析收藏纠错 + 选题
5. (2017九上·宜春期末) Rt△ABC中，∠C=90°，AC=8cm，BC=6cm，以点C为圆心5cm为半径的圆与直线AB的位置关系是（）

A . 相交 B . 相切 C . 相离 D . 无法确定

答案解析收藏纠错 + 选题
6. (2017九上·宜春期末) 二次函数y=ax²+b与反比例函数y= $\text{[math]}$ 在同一平面直角坐标系中的图象可能是（）

A . B . C . D .

答案解析收藏纠错 + 选题

二、填空题

7. (2017九上·宜春期末) 已知点A（9，a）和点B（b，﹣2）关于原点对称，则b^a=．

答案解析收藏纠错 + 选题
8. (2017九上·宜春期末) 设一元二次方程x²﹣3x﹣1=0的两根为m，n，则mn=

答案解析收藏纠错 + 选题
9. (2017九上·宜春期末) 在一个不透明的布袋中，红色、黑色、白色的玻璃球共有20个，除颜色外其他完全相同．小明通过多次摸球试验后发现其中摸到红色、黑色球的频率分别稳定在15%和45%，则口袋中白色球很可能有个．

答案解析收藏纠错 + 选题
10. (2017九上·宜春期末) 将抛物线y=x²﹣4x+1向左平移2个单位，再向上平移3个单位所得抛物线解析式为．

答案解析收藏纠错 + 选题
11. (2017九上·宜春期末) 如图，正方形ABCD内接于⊙O，弦BC所对的圆周角的度数为．

答案解析收藏纠错 + 选题
12. (2017九上·宜春期末) 二次函数y=ax²+bx+c（a≠0）的图象如图（虚线部分为对称轴），给出以下5个结论：①x≤1时，y随x的增大而增大；②abc＞0；③b＜a+c；④4a+2b+c＞0；⑤3a﹣b＜0，其中正确的结论有（填上所有正确结论的序号）．

答案解析收藏纠错 + 选题

三、解答题。

13. (2017九上·宜春期末) 解方程：4（x﹣1）=x（x﹣1）

答案解析收藏纠错 + 选题
14. (2017九上·宜春期末) 如图，AB是⊙O的直径， $\text{[math]}$ = $\text{[math]}$ ，且AB=5，BD=4，求弦DE的长．

答案解析收藏纠错 + 选题
15. (2017九上·宜春期末) 如图，一次函数y₁=x+1的图象与反比例函数y₂= $\text{[math]}$ （k为常数，且k≠0）的图象都经过点A（m，2），求反比例函数的解析式，并根据图象比较y₁和y₂的大小（x＞0）．

答案解析收藏纠错 + 选题
16. (2017九上·宜春期末) 如图，在边长为1的正方形网格中，△AOB的顶点均在格点上，点A、B的坐标分别是A（3，2）、B（1，3）．将△AOB绕点O逆时针旋转90°后得到△A₁OB₁ ．
1. （1）画出旋转后的△A₁OB₁ ，点A₁的坐标为；
2. （2）在旋转过程中，点B经过的路径为 $\text{[math]}$ ，求 $\text{[math]}$ 的长．
答案解析收藏纠错 + 选题
17. (2017九上·宜春期末) 已知关于x的方程x²+ax+a﹣2=0．
1. （1）求证：不论a取何实数，该方程都有两个不相等的实数根；
2. （2）若该方程有一根是﹣2，求另一根．
答案解析收藏纠错 + 选题
18. (2017九上·宜春期末) 已知△ABC内接于⊙O，请仅用无刻度的直尺，根据下列条件分别在图1，图2中画出∠BAC的平分线（保留作图痕迹，不写作法）．
1. （1）如图1，P是BC边的中点；
2. （2）如图2，直线l与⊙O相切于点P，且l∥BC．
答案解析收藏纠错 + 选题
19. (2017九上·宜春期末) 小源的父母决定中考之后带她去旅游，初步商量有意向的四个景点分别为：A．明月山，B．庐山，C．婺源，D．三清山．由于受到时间限制，只能选两个景点，于是小源的父母决定通过抽签选择，用四张小纸条分别写上四个景点做成四个签（外表无任何不同），让小源随机抽两次，每次抽一个签，每个签抽到的机会相等．
1. （1）小源最希望去婺源，则小源第一次恰好抽到婺源的概率是多少；
2. （2）除婺源外，小源还希望去明月山，求小源抽到婺源、明月山两个景点中至少一个的概率是多少．（通过“画树状图”或“列表”进行分析）
答案解析收藏纠错 + 选题
20. (2021九上·大余期末) 如图，点B、C、D都在半径为4的⊙O上，过点C作AC∥BD交OB的延长线于点A，连接CD，已知∠CDB=∠OBD=30°．
1. （1）求证：AC是⊙O的切线；
2. （2）求弦BD的长．
答案解析收藏纠错 + 选题
21. (2017九上·宜春期末) 寒假里，小斌与爸爸一起销售一种农产品体验生活．已知这种农产品的成本价为每千克20元，根据爸爸的经验，该农产品每天的销售量y（千克）与销售价x（元/千克）有如下关系：y=﹣2x+80．设该农产品每天的销售利润为w元．
1. （1）求w与x之间的函数关系式；
2. （2）爸爸说：“物价部门规定这种农产品的销售价不得高于每千克28元”，爸爸想要每天获得150元的销售利润，销售价应定为每千克多少元．
答案解析收藏纠错 + 选题
22. (2017九上·宜春期末) 冬天来了，晒衣服成了头疼的事情，聪明的小华想到一个好办法，在家后院地面（BD）上立两根等长的立柱AB、CD（均与地面垂直），并在立柱之间悬挂一根绳子．由于挂的衣服比较多，绳子的形状近似成了抛物线y=ax²﹣0.8x+c，如图1，已知立柱AB=CD=2.6米，BD=8米．
1. （1）求绳子最低点离地面的距离；
2. （2）为了防止衣服碰到地面，小华在离AB为3米的位置处用一根垂直于地面的立柱MN撑起绳子（如图2），使左边抛物线F₁的最低点距MN为1米，离地面1.6米，求MN的长．
答案解析收藏纠错 + 选题
23. (2021九上·大余期末) 已知∠α的顶点在正n边形的中心点O处，∠α绕着顶点O旋转，角的两边与正n边形的两边分别交于点M、N，∠α与正n边形重叠部分面积为S．
1. （1）
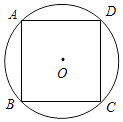
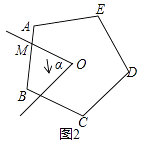
  当n=4，边长为2，∠α=90°时，如图（1），请直接写出S的值；
2. （2）
  当n=5，∠α=72°时，如图（2），请问在旋转过程中，S是否发生变化？并说明理由；
3. （3）
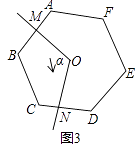
  当n=6，∠α=120°时，如图（3），请猜想S是原正六边形面积的几分之几（不必说明理由）．若∠α的平分线与BC边交于点P，判断四边形OMPN的形状，并说明理由．
答案解析收藏纠错 + 选题
24. (2017九上·宜春期末) 已知抛物线y=ax²﹣4ax+b与x轴的一个交点A的坐标为（3，0），与y轴交于点C．
1. （1）求抛物线与x轴的另一个交点B的坐标；
2. （2）当a=﹣1时，将抛物线向上平移m个单位后经过点（5，﹣7）．
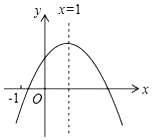
  ①求m的值及平移前、后抛物线的顶点P、Q的坐标．
  ②设平移后抛物线与y轴交于点D，问：在平移后的抛物线上是否存在点E，使得△ECD的面积是△EPQ的3倍？若存在，请求出点E的坐标；若不存在，请说明理由．
答案解析收藏纠错 + 选题