北京市海淀区2018-2019学年九年级上学期数学期中考试试...

更新时间：2024-07-13 浏览次数：466 类型：期中考试

一、选择题

1. (2019九上·海淀期中) 抛物线y=x²+1的对称轴是（）

A . 直线 B . 直线 C . 直线 D . 直线

答案解析收藏纠错 + 选题
2. (2019九上·海淀期中) 点P（2，-1）关于原点对称的点P′的坐标是（）

A . B . C . D .

答案解析收藏纠错 + 选题
3. (2020·中模拟) 下列App图标中，既不是中心对称图形也不是轴对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
4. (2019九上·海淀期中) 用配方法解方程x²-2x-4=0，配方正确的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
5. (2019九上·海淀期中) 如图，以O为圆心的两个同心圆中，大圆的弦AB是小圆的切线，点P为切点．若大圆半径为2，小圆半径为1，则AB的长为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$

D . 2

答案解析收藏纠错 + 选题
6. (2019九上·海淀期中) 将抛物线y=（x+1）²-2向上平移a个单位后得到的抛物线恰好与x轴有一个交点，则a的值为（）

A . $\text{[math]}$ B . 1 C . $\text{[math]}$ D . 2

答案解析收藏纠错 + 选题
7. (2019九上·海淀期中) 如图是几种汽车轮毂的图案，图案绕中心旋转90°后能与原来的图案重合的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
8. (2019九上·海淀期中) 已知一个二次函数图象经过P₁（-3，y₁），P₂（-1，y₂），P₃（1，y₃），P₄（3，y₄）四点，若y₃＜y₂＜y₄ ，则y₁ ， y₂ ， y₃ ， y₄的最值情况是（）

A . 最小，最大 B . 最小，最大 C . 最小，最大 D . 无法确定

答案解析收藏纠错 + 选题

二、填空题

9. (2022九上·朝阳月考) 写出一个以0和2为根的一元二次方程：．

答案解析收藏纠错 + 选题
10. (2019九上·海淀期中) 若二次函数y=ax²+bx+c的图象如图所示，则ac0（填“＞”或“=”或“＜”）．

答案解析收藏纠错 + 选题
11. (2019九上·海淀期中) 若关于x的方程x²-4x+k-1=0有两个不相等的实数根，则k的取值范围是．

答案解析收藏纠错 + 选题
12. (2019九上·西城期中) 如图，四边形ABCD内接于⊙O，E为直径CD延长线上一点，且AB∥CD，若∠C=70°，则∠ADE的大小为．

答案解析收藏纠错 + 选题
13. (2019九上·海淀期中) 已知O为△ABC的外接圆圆心，若O在△ABC外，则△ABC是（填“锐角三角形”或“直角三角形”或“钝角三角形”）．

答案解析收藏纠错 + 选题
14. (2019九上·海淀期中) 在十三届全国人大一次会议记者会上，中国科技部部长表示，2017年我国新能源汽车保有量已居于世界前列.2015年和2017年我国新能源汽车保有量如图所示．设我国2015至2017年新能源汽车保有量年平均增长率为x，依题意，可列方程为．

答案解析收藏纠错 + 选题
15. (2019九上·海淀期中) 如图，在平面直角坐标系xOy中，抛物线y=ax²+bx+c与x轴交于（1，0），（3，0）两点，请写出一个满足y＜0的x的值．

答案解析收藏纠错 + 选题
16. (2019九上·海淀期中) 如图，⊙O的动弦AB，CD相交于点E，且AB=CD，∠BED=α（0°＜α＜90°）．在①∠BOD=α，②∠OAB=90°-α，③∠ABC= $\text{[math]}$ α中，一定成立的是（填序号）．

答案解析收藏纠错 + 选题

三、计算题

17. (2020九上·青岛月考) 解方程：x（x+2）=3x+6．

答案解析收藏纠错 + 选题

四、解答题

18. (2022八下·凤县期中) 如图，将△ABC绕点B旋转得到△DBE，且A，D，C三点在同一条直线上．求证：DB平分∠ADE．

答案解析收藏纠错 + 选题
19. (2019九上·海淀期中) 下面是小董设计的“作已知圆的内接正三角形”的尺规作图过程．
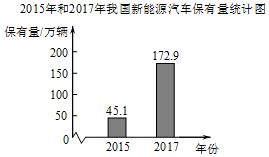
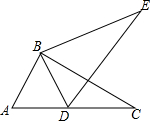
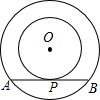
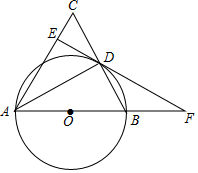
已知：⊙O．

求作：⊙O的内接正三角形．

作法：如图，

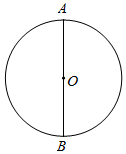
作直径AB；

②以B为圆心，OB为半径作弧，与⊙O交于C，D两点；

③连接AC，AD，CD．

所以△ACD就是所求的三角形．

根据小董设计的尺规作图过程，
1. （1）使用直尺和圆规，补全图形；（保留作图痕迹）
2. （2）完成下面的证明：
  证明：在⊙O中，连接OC，OD，BC，BD，
  
  ∵OC=OB=BC，
  
  ∴△OBC为等边三角形（）（填推理的依据）．
  
  ∴∠BOC=60°．
  
  ∴∠AOC=180°-∠BOC=120°．
  
  同理∠AOD=120°，
  
  ∴∠COD=∠AOC=∠AOD=120°．
  
  ∴AC=CD=AD（）（填推理的依据）．
  
  ∴△ACD是等边三角形．
答案解析收藏纠错 + 选题
20. (2019九上·海淀期中) 已知-1是方程x²+ax-b=0的一个根，求a²-b²+2b的值．

答案解析收藏纠错 + 选题
21. (2019九上·海淀期中) 生活中看似平常的隧道设计也很精巧．如图是一张盾构隧道断面结构图，隧道内部为以O为圆心AB为直径的圆．隧道内部共分为三层，上层为排烟道，中间为行车隧道，下层为服务层．点A到顶棚的距离为0.8a，顶棚到路面的距离是3.2a，点B到路面的距离为2a．请你求出路面的宽度l．（用含a的式子表示）

答案解析收藏纠错 + 选题
22. (2019九上·海淀期中) 如图，在平面直角坐标系xOy中，抛物线y=x²+ax+b经过点A（-2，0），B（-1，3）．
1. （1）求抛物线的解析式；
2. （2）设抛物线的顶点为C，直接写出点C的坐标和∠BOC的度数．
答案解析收藏纠错 + 选题
23. (2023九上·越城月考) 如图，用长为6m的铝合金条制成“日”字形窗框，若窗框的宽为x m，窗户的透光面积为y m²（铝合金条的宽度不计）．
1. （1）求出y与x的函数关系式；
2. （2）如何安排窗框的长和宽，才能使得窗户的透光面积最大？并求出此时的最大面积．
答案解析收藏纠错 + 选题
24. (2020九上·北京月考) 如图，在△ABC中，AB=AC，以AB为直径作⊙O交BC于点D，过点D作AC的垂线交AC于点E，交AB的延长线于点F．
1. （1）求证：DE与⊙O相切；
2. （2）若CD=BF，AE=3，求DF的长．
答案解析收藏纠错 + 选题
25. (2019九上·海淀期中) 有这样一个问题：探究函数y= $\text{[math]}$ 的图象与性质．
小东根据学习函数的经验，对函数y= $\text{[math]}$ 的图象与性质进行了探究．

下面是小东的探究过程，请补充完成：
1. （1）化简函数解析式，当x≥3时，y=，当x＜3时y=；
2. （2）根据（1）中的结果，请在所给坐标系中画出函数y= $\text{[math]}$ 的图象；
3. （3）结合画出的函数图象，解决问题：若关于x的方程ax+1= $\text{[math]}$ 只有一个实数根，直接写出实数a的取值范围：．
答案解析收藏纠错 + 选题
26. (2019九上·海淀期中) 在平面直角坐标系xOy中，抛物线y=ax²-2x（a≠0）与x轴交于点A，B（点A在点B的左侧）．
1. （1）当a=-1时，求A，B两点的坐标；
2. （2）过点P（3，0）作垂直于x轴的直线l，交抛物线于点C．
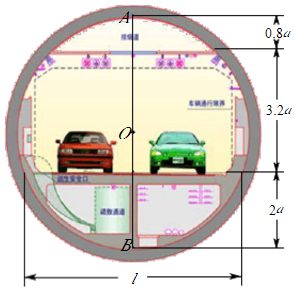
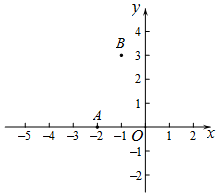
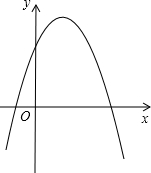
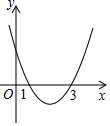
  ①当a=2时，求PB+PC的值；
  
  ②若点B在直线l左侧，且PB+PC≥14，结合函数的图象，直接写出a的取值范围．
答案解析收藏纠错 + 选题
27. (2019九上·海淀期中) 已知∠MON=α，P为射线OM上的点，OP=1．
1. （1）如图1，α=60°，A，B均为射线ON上的点，OA=1，OB＞OA，△PBC为等边三角形，且O，C两点位于直线PB的异侧，连接AC．
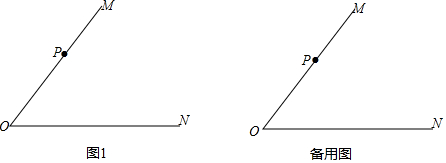
  ①依题意将图1补全；
  
  ②判断直线AC与OM的位置关系并加以证明；
2. （2）若α=45°，Q为射线ON上一动点（Q与O不重合），以PQ为斜边作等腰直角△PQR，使O，R两点位于直线PQ的异侧，连接OR．根据（1）的解答经验，直接写出△POR的面积．
答案解析收藏纠错 + 选题
28. (2019九上·海淀期中) 在平面直角坐标系xOy中，点A是x轴外的一点，若平面内的点B满足：线段AB的长度与点A到x轴的距离相等，则称点B是点A的“等距点”．
1. （1）若点A的坐标为（0，2），点P₁（2，2），P₂（1，-4），P₃（- $\text{[math]}$ ，1）中，点A的“等距点”是；
2. （2）若点M（1，2）和点N（1，8）是点A的两个“等距点”，求点A的坐标；
3. （3）记函数y= $\text{[math]}$ x（x＞0）的图象为L，⊙T的半径为2，圆心坐标为T（0，t）．若在L上存在点M，⊙T上存在点N，满足点N是点M的“等距点”，直接写出t的取值范围．
答案解析收藏纠错 + 选题