 B .
B .  C .
C . 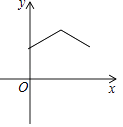 D .
D . 








如图,在平面直角坐标系中,已知Rt△AOB的两直角边OA,OB分别在x轴,y轴的正半轴上(OA<OB),且OA,OB的长分别是一元二次方程x2﹣14x+48=0的两个根,线段AB的垂直平分线CD交AB于点C,分别交x轴,y轴于点D,E.

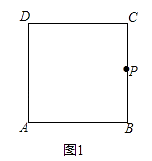
如图1,若△ABC的一个边共相似点P与其对角顶点B的连线,将△ABC分割成的两个三角形恰与原三角形均相似,试判断△ABC的形状,并说明理由.

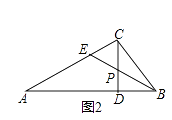
如图2,在△ABC中,∠A<∠B<∠C,高线CD与角平分线BE交于点P,若P是△ABC的一个内共相似点,试说明点E是△ABC的边共相似点,并直接写出∠A的度数.
如图3,在Rt△ABC中,∠C=90°,∠A=30°,BC= ,若△PBC与△ABC相似,则满足条件的P点共有个,顺次连接所有满足条件的P点而围成的多边形的周长为.
