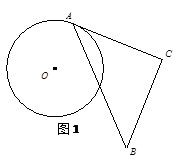江苏省江阴市长泾片2019届九年级上学期数学期中考试试卷

更新时间：2019-02-26 浏览次数：368 类型：期中考试

一、单选题

1. (2018九上·江阴期中) 方程x²－2x＝0的根是（）

A . x₁＝0，x₂＝2 B . x₁＝0，x₂＝－2 C . x＝0 D . x＝2

答案解析收藏纠错 + 选题
2. (2018九上·江阴期中) 下列一元二次方程中，两根之和为-1的是（）

A . x²+x+2=0 B . x²－x－5=0 C . x²+x－3=0 D . 2 x²－x－1=0

答案解析收藏纠错 + 选题
3. (2018九上·江阴期中) 已知 $\text{[math]}$ = $\text{[math]}$ ，那么下列等式中不一定正确的是（）

A . 2x=5y B . = $\text{[math]}$ C . = D . = $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2018九上·江阴期中) 若△ABC∽△A′B′C′，∠A=40°，∠C=110°，则∠B′等于（　　）

A . 30° B . 50° C . 40° D . 70°

答案解析收藏纠错 + 选题
5. (2018九上·江阴期中) 为了解某社区居民的用电情况，随机对该社区10户居民进行了调查，下表是这10户居民2014年4月份用电量的调查结果：
居民（户）
1
3
2
4
月用电量（度/户）
40
50
55
60
那么关于这10户居民月用电量（单位：度），下列说法错误的是（）

A . 中位数是55 B . 众数是60 C . 方差是29 D . 平均数是54

答案解析收藏纠错 + 选题
6. (2018九上·江阴期中) 如图，在△ABC中，点D，E分别在边AB，AC上，且 $\text{[math]}$ ，则S_△_ADE∶S_四边形_BCED的值为（）

A . 1∶ $\text{[math]}$ B . 1∶3 C . 1∶8 D . 1∶9

答案解析收藏纠错 + 选题
7. (2018九上·江阴期中) 如图，△AOB是直角三角形，∠AOB＝90°，OB＝2OA，点A在反比例函数y＝ $\text{[math]}$ 的图象上．若点B在反比例函数y＝ $\text{[math]}$ 的图象上，则k的值为（）

A . －4 B . 4 C . －2 D . 2

答案解析收藏纠错 + 选题
8. (2018九上·江阴期中) 如图，△ABC内接于⊙O，∠BAC=120°，AB=AC，BD为⊙O的直径，AB=3，则AD的值为（）

A . 6 B . C . 5 D .

答案解析收藏纠错 + 选题
9. (2018九上·江阴期中) 如图，在△ABC中，AC=BC，CD是AB边上的高线，且有2CD=3AB，又E，F为CD的三等分点，则∠ACB与∠AEB之和为（）

A . 45° B . 90° C . 75° D . 135°

答案解析收藏纠错 + 选题
10. (2018九上·江阴期中) 如图，已知AB=12，点C、D在AB上，且AC=DB=2，点P从点C沿线段CD向点D运动（运动到点D停止），以AP、BP为斜边在AB的同侧画等腰Rt△APE和等腰Rt△PBF，连接EF，取EF的中点G，下列说法中正确的有（）
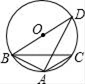
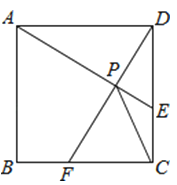
①△EFP的外接圆的圆心为点G；②四边形AEFB的面积不变；③EF的中点G移动的路径长为4．

A . 0个 B . 1个 C . 2个 D . 3个

答案解析收藏纠错 + 选题

二、填空题

11. (2018九上·江阴期中) 直接写出解： $\text{[math]}$ ；
若 $\text{[math]}$ ，则 $\text{[math]}$ 。

答案解析收藏纠错 + 选题
12. (2018九上·江阴期中) 若方程（n－1）x²－3x＋1＝0是关于x的一元二次方程，则n需满足．

答案解析收藏纠错 + 选题
13. (2018九上·江阴期中) 在比例尺为1:5000的江阴市城区地图上，某段路的长度约为25厘米，则它的实际长度约为米

答案解析收藏纠错 + 选题
14. (2020九下·广陵月考) 用一个圆心角120°，半径为9的扇形作一个圆锥的侧面，圆锥的底面圆半径是

答案解析收藏纠错 + 选题
15. (2018九上·江阴期中) 在Rt△ABC中，∠C＝90°，AC＝2 ， BC＝4，若以点C为圆心，AC为半径作圆，则AB边的中点E与⊙C的位置关系为．

答案解析收藏纠错 + 选题
16. (2018九上·江阴期中) 如图，将含有60°角的直角三角尺ABC绕顶点A顺时针旋转45°度后得到△AB′C′，点B经过的路径为弧BB′，若∠BAC=60°，AC=1，则图中阴影部分的面积是

答案解析收藏纠错 + 选题
17. (2018九上·江阴期中) 如图，△ABC中，AB=BC，AC=8，点F是△ABC的重心（即点F是△ABC的两条中线AD、BE的交点），BF=6，则DF=．

答案解析收藏纠错 + 选题
18. (2020·广西模拟)
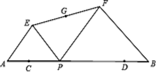
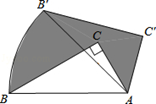
如图，在正方形ABCD中，动点E，F分别从D，C两点同时出发，以相同的速度在边DC，CB上移动，连接AE和DF交于点P，由于点E，F的移动，使得点P也随之运动．若AD=2，线段CP的最小值是．

答案解析收藏纠错 + 选题

三、解答题

19. (2018九上·江阴期中) 解方程
1. （1） x²﹣4x+1=0（用配方法）；
2. （2） 3x(x－1)=2－2x
3. （3） $\text{[math]}$
4. （4） x²﹣3x=2
答案解析收藏纠错 + 选题
20. (2018九上·江阴期中) 已知：△ABC在直角坐标平面内，三个顶点的坐标分别为A（0，3）、B（3，4）、C（2，2）（正方形网格中每个小正方形的边长是一个单位长度）．
1. （1） △ABC向下平移4个单位长度得到的△A₁B₁C₁ ，点C₁的坐标是；
2. （2）以点B为位似中心，在网格内画出△A₂B₂C₂ ，使△A₂B₂C₂与△ABC位似，且位似比为2：1，点C₂的坐标是；（画出图形）
3. （3） △A₂B₂C₂的面积是平方单位．
答案解析收藏纠错 + 选题
21. (2018九上·江阴期中) 已知关于x的一元二次方程x²＋(2m－1)x＋m²＝0有两个实数根x₁、x₂ ，并且满足x₁²＋x₂²＝1，求m的值.

答案解析收藏纠错 + 选题
22. (2018九上·江阴期中) 如图：
1. （1）如图①，用尺规作图作出圆的一条直径EF（不写作法，保留作图痕迹）；
2. （2）如图②，A、B、C、D为圆上四点，AB∥CD，AB＜CD，请只用无刻度的直尺，画出圆的一条直径EF（不写画法，保留画图痕迹）．
答案解析收藏纠错 + 选题
23. (2024九上·黄埔期末) 如图，在△ABC中，∠ABC=90°，D是边AC上的一点，连接BD，使∠A=2∠1，E是BC上的一点，以BE为直径的⊙O经过点D．
1. （1）求证：AC是⊙O的切线；
2. （2）若∠A=60°，⊙O的半径为2，求阴影部分的面积．（结果保留根号和π）．
答案解析收藏纠错 + 选题
24. (2018九上·江阴期中) 在“文化南长•全民阅读”活动中，某中学社团“清风读书社”对全校学生的人数及纸质图书阅读量（单位：本）进行了调查.2016年全校有1000名学生，2017年全校学生人数比2016年增加10%，2018年全校学生人数比2017年增加100人．
1. （1） 2018年全校学生有人；
2. （2） 2017年全校学生人均阅读量比2016年多1本，阅读总量比2016年增加1700本．
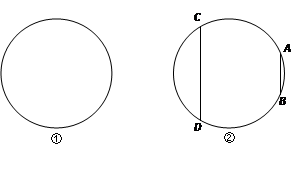
  （注：阅读总量=人均阅读量×人数）
  
  ①求2016年全校学生人均阅读量；
  
  ②2016年读书社人均阅读量是全校学生人均阅读量的2.5倍，如果2017年、2018年这两年读书社人均阅读量都比前一年增长一个相同的百分数a，2018年全校学生人均阅读量比2016年增加的百分数也是a，那么2018年读书社全部80名成员的阅读总量将达到全校学生阅读总量的25%，求a的值．
答案解析收藏纠错 + 选题
25. (2018九上·江阴期中) 我们新定义一种三角形：两边平方和等于第三边平方的两倍的三角形叫做奇异三角形．
1. （1）根据“奇异三角形”的定义，请你判断命题“等边三角形一定是奇异三角形”是真命题还是假命题?
2. （2）在Rt△ABC中，∠ACB=90°，AB=c，AC=b，BC=a，且b＞a，若Rt△ABC是奇异三角形，求a：b：c；
3. （3）如图，AB是⊙O的直径，点C是⊙O上一点（不与点A，B重合），D是半圆 $\text{[math]}$ 的中点，C，D在直径AB的两侧，若在⊙O内存在点E，使AE=AD，CB=CE．
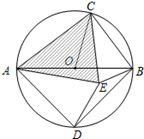
  求证：△ACE是奇异三角形．
答案解析收藏纠错 + 选题
26. (2018九上·江阴期中) 阅读下面材料：
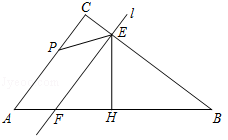
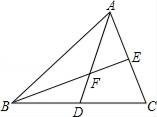
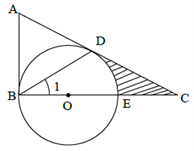
小昊遇到这样一个问题：如图1，在△ABC中，∠ACB=90°，BE是AC边上的中线，点D在BC边上，CD：BD=1：2，AD与BE相交于点P，求 $\text{[math]}$ 的值．
1. （1）小昊发现，过点A作AF∥BC，交BE的延长线于点F，通过构造△AEF，经过推理和计算能够使问题得到解决（如图2）．请回答： $\text{[math]}$ 的值为．
2. （2）参考小昊思考问题的方法，解决问题：
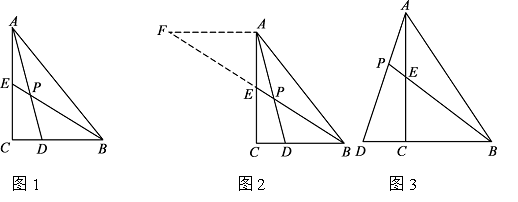
  如图 3，在△ABC中，∠ACB=90°，点D在BC的延长线上，AD与AC边上的中线BE的延长线交于点P，DC：BC：AC=1：2：3 ．
  
  ①求 $\text{[math]}$ 的值；
  
  ②若CD=2，则BP=．
答案解析收藏纠错 + 选题
27. (2019九上·宜兴期中) 将一块含有45°的三角板ABC的顶点A放在⊙O上，且AC与⊙O相切于点A（如图1），将△ABC从点A开始，绕着点A顺时针旋转，设旋转角为α（0°＜α＜135°），旋转后，AC、AB分别与⊙O交于点E，F，连接EF（如图2）．已知AC=8，⊙O的半径为4．
1. （1）在旋转过程中，有以下几个量：①弦EF的长；② $\text{[math]}$ 的长；③∠AFE的度数；④点O到EF的距离．其中不变的量是（填序号）；
2. （2）当α＝°时，BC与⊙O相切（直接写出答案）；
3. （3）当BC与⊙O相切时，求△AEF的面积．
答案解析收藏纠错 + 选题
28. (2018九上·江阴期中) 如图，在Rt△ABC中，∠C=90°，AC=6，BC=8．动点P从点A开始沿折线AC﹣CB﹣BA运动，点P在AC，CB，BA边上运动的速度分别为每秒3，4，5个单位．直线l从与AC重合的位置开始，以每秒 $\text{[math]}$ 个单位的速度沿CB方向移动，移动过程中保持l∥AC，且分别与CB，AB边交于E，F两点，点P与直线l同时出发，设运动的时间为t秒，当点P第一次回到点A时，点P和直线l同时停止运动．
1. （1）当t=5秒时，点P走过的路径长为；当t=秒时，点P与点E重合；
2. （2）当点P在AC边上运动时，连结PE，并过点E作AB的垂线，垂足为H．若以C、P、E为顶点的三角形与△EFH相似，试求线段EH的值；
3. （3）当点P在折线AC﹣CB﹣BA上运动时，作点P关于直线EF的对称点Q．在运动过程中，若形成的四边形PEQF为菱形，求t的值．
答案解析收藏纠错 + 选题