江苏省无锡市宜兴市丁蜀学区2020届九年级上学期数学期中考试...

更新时间：2019-12-22 浏览次数：234 类型：期中考试

一、单选题

1. (2024八下·环翠期中) 下列关于 $\text{[math]}$ 的方程中，一定是一元二次方程的为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2019九上·宜兴期中) 若一元二次方程x²+x－2=0的解为x₁、x₂ ，则x₁•x₂的值是（）

A . 1 B . —1 C . 2 D . —2

答案解析收藏纠错 + 选题
3. (2024九上·茂名期末) 如图，在⊙O中，∠ABC=50°，则∠AOC等于（）

A . 50° B . 80° C . 90° D . 100°

答案解析收藏纠错 + 选题
4. (2019九上·宜兴期中) 下列说法正确的是（）

A . 等弧所对的圆心角相等 B . 优弧一定大于劣弧 C . 经过三点可以作一个圆 D . 相等的圆心角所对的弧相等

答案解析收藏纠错 + 选题
5. (2019九上·宜兴期中) 如图为4×4的正方形网格，A，B，C，D，O均在格点上，点O是（）

A . △ACD的外心 B . △ABC的外心 C . △ACD的内心 D . △ABC的内心

答案解析收藏纠错 + 选题
6. (2019九上·宜兴期中) 如图，⊙O的半径OC=5cm，直线l⊥OC，垂足为H，且 $\text{[math]}$ 交⊙O于A、B两点，AB=8cm，则l沿OC所在直线平移后与⊙O相切，则平移的距离是（）

A . 2cm或8cm B . 2cm C . 1cm 或8cm D . 1cm

答案解析收藏纠错 + 选题
7. (2021八下·龙口期中) 若关于x的一元二次方程nx²﹣2x﹣1=0无实数根，则一次函数y=（n+1）x﹣n的图象不经过（）

A . 第一象限 B . 第二象限 C . 第三象限 D . 第四象限

答案解析收藏纠错 + 选题
8. (2019九上·宜兴期中) 如图，在Rt△AOB中，∠AOB=90°，OA=3，OB=2，将Rt△AOB绕点O顺时针旋转90°后得Rt△FOE，将线段EF绕点E逆时针旋转90°后得线段ED，分别以O，E为圆心，OA、ED长为半径画弧AF和弧DF，连接AD，则图中阴影部分面积是（）

A . π B . $\text{[math]}$ C . 3+π D . 8﹣π

答案解析收藏纠错 + 选题
9. (2020九上·沭阳期中) 如图，在平面直角坐标系xOy中，以原点O为圆心的圆过点A(13，0)直线y=kx-3k+4与 $\text{[math]}$ 交于B、C两点，则弦BC的长的最小值为（）

A . 22 B . 24 C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题

10. (2021九上·南岗开学考) 若关于x的一元二次方程（m﹣1）x²+x+m²﹣1＝0有一个根为0，则m的值为.

答案解析收藏纠错 + 选题
11. (2019八下·诸暨期中) 某公司在年的盈利额为万元，预计年的盈利额将达到万元，若每年比上一年盈利额增长的百分率相同，那么该公司在年的盈利额为万元.

答案解析收藏纠错 + 选题
12. (2020九上·江阴月考) 在比例尺为1∶50000的地图上，量得A、B两地的图上距离AB＝3cm，则A、B两地的实际距离为km.

答案解析收藏纠错 + 选题
13. (2024九下·岳阳开学考) 相邻两边长的比值是黄金分割数的矩形，叫做黄金矩形，从外形看，它最具美感．现在想要制作一张“黄金矩形”的贺年卡，如果较长的一条边长等于20厘米，那么相邻一条边的边长等于厘米．

答案解析收藏纠错 + 选题
14. (2019九上·宜兴期中) 一个底面直径是10cm,母线长为15cm的圆锥，它的侧面积为cm².

答案解析收藏纠错 + 选题
15. (2019九上·宜兴期中) 如图，AB 为⊙O 的直径，弦CD⊥AB 于E，已知CD=12，BE=3，则⊙O 的直径为

答案解析收藏纠错 + 选题
16. (2019九上·宜兴期中) 把直尺、三角尺和圆形螺母按如图所示放置于桌面上，∠CAB=60°，若量出AD=6cm，则圆形螺母的外直径是.

答案解析收藏纠错 + 选题
17. (2019九上·宜兴期中) 如图，已知直线y= $\text{[math]}$ x﹣3与x轴、y轴分别交于A、B两点，P在以C（0，1）为圆心，1为半径的圆上一动点，连结PA、PB，则△PAB面积的最大值是．

答案解析收藏纠错 + 选题

三、解答题

18. (2019九上·宜兴期中) 解一元二次方程：
1. （1）（2x﹣5）²=9
2. （2） x²﹣4x=96
3. （3） 3x²+5x﹣2=0
4. （4） 2（x﹣3）²=﹣x（3﹣x）
答案解析收藏纠错 + 选题
19. (2024八下·苏州工业园月考) 先化简，再求值： $\text{[math]}$ ，其中 $\text{[math]}$ 满足 $\text{[math]}$ .

答案解析收藏纠错 + 选题
20. (2023九上·南昌期中) 已知： $\text{[math]}$ ABCD的两边AB，AD的长是关于x的方程 $\text{[math]}$ 的两个实数根.
1. （1）当m为何值时，四边形ABCD是菱形？求出这时菱形的边长；
2. （2）若AB的长为2，那么 $\text{[math]}$ ABCD的周长是多少？
答案解析收藏纠错 + 选题
21. (2023九上·兰溪月考) 如图所示，AB为☉O的直径，CD是☉O的弦，AB，CD的延长线交于点E，已知AB=2DE，∠AEC=20°.求∠AOC的度数.

答案解析收藏纠错 + 选题
22. (2019九上·宜兴期中) 如图，在Rt△ABC中，∠ACB＝90°，AC＝6，CB＝8，AD是△ABC的角平分线，过A、C、D三点的圆与斜边AB交于点E，连接DE。
1. （1）求证：AC＝AE；
2. （2）求△ACD外接圆的直径。
答案解析收藏纠错 + 选题
23. (2019九上·宜兴期中) 问题提出：如图，已知：线段AB，试在平面内找到符合条件的所有点C，

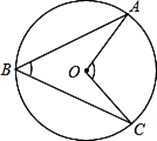
使∠ACB=30°。（利用直尺和圆规作图，保留作图痕迹，不写作法).

尝试解决：为了解决这个问题，下面给出一种解题思路：先作出等边三角形AOB，然后以点O 为圆心，OA长为半径作⊙O，则优弧AB上的点即为所要求作的点（点A、B除外），根据对称性，在AB的另一侧符合条件的点C易得。请根据提示，完成作图.

自主探索：在平面直角坐标系中，已知点A(3，0)、B(－1，0)，点C是y轴上的一个动点，当∠BCA=45°时，求点C的坐标

答案解析收藏纠错 + 选题
24. (2019九上·宜兴期中) 如图，在平面直角坐标系中，点A、C的坐标分别为（0，8）、（6，0），以AC为直径作⊙O，交坐标轴于点B，点D是⊙O 上一点，且 $\text{[math]}$ ，过点D作DE⊥BC，垂足为E.
1. （1）求证：CD平分∠ACE；
2. （2）判断直线ED与⊙O的位置关系，并说明理由；
3. （3）求线段CE的长.
答案解析收藏纠错 + 选题
25. (2019九上·宜兴期中) 某校八年级学生小阳，小杰和小凡到某超市参加了社会实践活动，在活动中他们参与了某种水果的销售工作，已知该水果的进价为10元/千克，下面是他们在活动结束后的对话.
小阳：如果以12元/千克的价格销售，那么每天可售出300千克.

小杰：如果以15元/千克的价格销售，那么每天可获取利润750元.

小凡：我通过调查验证发现每天的销售量y（千克）与销售单价x（元）之间存在一次函数关系.
1. （1）求y（千克）与x（元）（x＞0）的函数关系式；
2. （2）当销售单价为何值时，该超市销售这种水果每天获得的利润达600元？
答案解析收藏纠错 + 选题
26. (2019九上·宜兴期中) 将一块含有45°的三角板ABC的顶点A放在⊙O上，且AC与⊙O相切于点A（如图1），将△ABC从点A开始，绕着点A顺时针旋转，设旋转角为α（0°＜α＜135°），旋转后，AC、AB分别与⊙O交于点E，F，连接EF（如图2）．已知AC=8，⊙O的半径为4．
1. （1）在旋转过程中，有以下几个量：①弦EF的长；② $\text{[math]}$ 的长；③∠AFE的度数；④点O到EF的距离．其中不变的量是（填序号）；
2. （2）当α＝°时，BC与⊙O相切（直接写出答案）；
3. （3）当BC与⊙O相切时，求△AEF的面积．
答案解析收藏纠错 + 选题
27. (2019九上·宜兴期中) 在平面直角坐标系 $\text{[math]}$ 中的点P和图形M，给出如下的定义：若在图形M存在一点Q，使得P、Q两点间的距离小于或等于1，则称P为图形M的关联点.
1. （1）当⊙O的半径为2时，
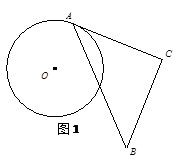
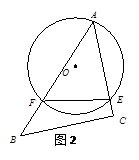
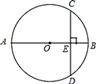
  ①在点 $\text{[math]}$ 中，⊙O的关联点.
  
  ②点P在直线y=-x上，若P为⊙O 的关联点，求点P的横坐标的取值范围.
2. （2） ⊙C 的圆心在x轴上，半径为2，直线y=-x+1与x轴、y轴交于点A、B.若线段AB上的所有点都是⊙C的关联点，直接写出圆心C的横坐标的取值范围.
答案解析收藏纠错 + 选题