河南省洛阳市洛宁县2018届九年级上学期数学期末考试试卷

更新时间：2024-07-13 浏览次数：276 类型：期末考试

一、单选题

1. (2018九上·洛宁期末) 化简 $\text{[math]}$ 的结果是（）

A . $\text{[math]}$ B . C . D .

答案解析收藏纠错 + 选题
2. (2018九上·连城期中) 一元二次方程2x²﹣5x﹣2=0的根的情况是（）

A . 有两个相等的实数根 B . 有两个不相等的实数根 C . 只有一个实数根 D . 没有实数根

答案解析收藏纠错 + 选题
3. (2018九上·洛宁期末) 用配方法解方程 x²+4x+1=0 时，经过配方，得到（）

A . B . C . D .

答案解析收藏纠错 + 选题
4. (2018九上·孟津期末) 某商场今年3月份的营业额为400万元，5月份的营业额达到633.6万元，若设商场3月份到5月份营业额的月平均增长率为x，则下面列出的方程中正确的是（）

A . 400（1+x）²=633.6 B . 400（1+2x）²=6336 C . 400×（1+2x）²=63.6 D . 400×（1+x）²=633.6+400

答案解析收藏纠错 + 选题
5. (2019九下·新乐开学考) 当A为锐角，且 $\text{[math]}$ ＜cosA＜ $\text{[math]}$ 时，∠A的范围是（　　）

A . 0°＜∠A＜30° B . 30°＜∠A＜60° C . 60°＜∠A＜90° D . 30°＜∠A＜45°

答案解析收藏纠错 + 选题
6. (2018九上·孟津期末) 如图，在△ABC中，点D、E分别是边AB，BC的中点．若△DBE的周长是6，则△ABC的周长是（）

A . 8 B . 10 C . 12 D . 14

答案解析收藏纠错 + 选题
7. (2018九上·洛宁期末) 如图1，在三角形纸片ABC中，∠A=78°，AB=4，AC=6．将△ABC沿图示中的虚线剪开，剪下的阴影三角形与原三角形相似的有（）

A . ①②③ B . ①②④ C . ①③④ D . ②③④

答案解析收藏纠错 + 选题
8. (2018九上·下城期中)
一个不透明的袋子里有若干个小球，它们除了颜色外，其它都相同，甲同学从袋子里随机摸出一个球，记下颜色后放回袋子里，摇匀后再次随机摸出一个球，记下颜色，…，甲同学反复大量实验后，根据白球出现的频率绘制了如图所示的统计图，则下列说法正确的是（　　）

A . 袋子一定有三个白球 B . 袋子中白球占小球总数的十分之三 C . 再摸三次球，一定有一次是白球 D . 再摸1000次，摸出白球的次数会接近330次

答案解析收藏纠错 + 选题
9. (2018九上·洛宁期末) 如图，面积为16的正方形ABCD中，有一个小正方形EFGH，其中E，F，G分别在AB，BC，FD上．若BF=1，则小正方形的周长为（）

A . 7 B . 6 C . 5 D . 4

答案解析收藏纠错 + 选题
10. (2018九上·洛宁期末) 我们知道：四边形具有不稳定性．如图，在平面直角坐标系中，边长为2的正方形ABCD的边AB在x轴上，AB的中点是坐标原点O，固定点A，B，把正方形沿箭头方向推，使点D落在y轴正半轴上点D′处，则点C的对应点C′的坐标为（）

A . （ $\text{[math]}$ ，1） B . （2，1） C . （1， $\text{[math]}$ ） D . （2， $\text{[math]}$ ）

答案解析收藏纠错 + 选题
11. (2018九上·洛宁期末) 在Rt△ABC中，D为斜边AB的中点，且BC=3，AC=4，则线段CD的长是（）

A . 2 B . 3 C . $\text{[math]}$ D . 5

答案解析收藏纠错 + 选题
12. (2018九上·洛宁期末) 计算 $\text{[math]}$ 的值等于（）

A . B . C . D . $\text{[math]}$

答案解析收藏纠错 + 选题
13. (2018九上·洛宁期末) 在Rt△ABC中，∠C=90°，AB=4， AC=1，则cosB的值为（）

A . B . $\text{[math]}$ C . D .

答案解析收藏纠错 + 选题
14. (2018九上·洛宁期末) 一个不透明的盒子中装有6个大小相同的乒乓球，其中4个是黄球，2个是白球．从该盒子中任意摸出一个球，摸到黄球的概率是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D .

答案解析收藏纠错 + 选题
15. (2018九上·洛宁期末) 同时投掷两枚硬币，出现两枚都是正面朝上的概率是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . 1 D . $\text{[math]}$

答案解析收藏纠错 + 选题
16. (2018九上·洛宁期末) 一副完整的扑克牌，去掉大小王，将剩余的52张混合后从中随机抽取一张，则抽出A的概率是（）

A . $\text{[math]}$ B . C . D .

答案解析收藏纠错 + 选题
17. (2018九上·洛宁期末) 要由抛物线 $\text{[math]}$ 平移得到 $\text{[math]}$ ，则平移的方法是（）

A . 向左平移1个单位 B . 向上平移1个单位 C . 向下平移1个单位 D . 向右平移1个单位

答案解析收藏纠错 + 选题
18. (2018九上·洛宁期末) 在二次函数 $\text{[math]}$ 的图象中，若 $\text{[math]}$ 随 $\text{[math]}$ 的增大而增大，则 $\text{[math]}$ 的取值范围是（）

A . x<1 B . x>1 C . x<-1 D . x>-1

答案解析收藏纠错 + 选题
19. (2018九上·洛宁期末) 抛物线y=（x﹣1）²+t与x轴的两个交点之间的距离为4，则t的值是（）

A . ﹣1 B . ﹣2 C . ﹣3 D . ﹣4

答案解析收藏纠错 + 选题

二、填空题

20. (2018九上·孟津期末) 二次根式 $\text{[math]}$ 有意义，则x取值范围．

答案解析收藏纠错 + 选题
21. (2018九上·孟津期末) 已知a：b=3：2，则(a-b)：a= ．

答案解析收藏纠错 + 选题
22. (2024七下·沂源期中) 有画有等腰三角形、平行四边形、等腰梯形、长方形、等边三角形五张卡片，背面朝下，颜色、形状、大小都一样，任取一张是中心对称图形的概率是．

答案解析收藏纠错 + 选题
23. (2018九上·洛宁期末) 如图，Rt△ABC中，∠ACB=90°，∠ABC=60°，BC=4cm，D为BC的中点，若动点E以1cm/s的速度从A点出发，沿着A→B→A的方向运动，设E点的运动时间为t秒（0≤t＜12），连接DE，当△BDE是直角三角形时，t的值为．

答案解析收藏纠错 + 选题
24. (2019·毕节模拟) 如图，D是等边△ABC边AB上的点，AD=2，DB=4．现将△ABC折叠，使得点C与点D重合，折痕为EF，且点E、F分别在边AC和BC上，则 $\text{[math]}$ =．

答案解析收藏纠错 + 选题
25. (2018九上·孟津期末) 如图，某城市的电视塔AB坐落在湖边，数学老师带领学生隔湖测量电视塔AB的高度，在点M处测得塔尖点A的仰角∠AMB为22.5°，沿射线MB方向前进200米到达湖边点N处，测得塔尖点A在湖中的倒影A′的俯角∠A′NB为45°，则电视塔AB的高度为米（结果保留根号）．

答案解析收藏纠错 + 选题
26. (2020八上·巴彦淖尔期中) 点（2+a，3）关于y轴对称的点的坐标是（﹣4，2﹣b），则a^b=．

答案解析收藏纠错 + 选题
27. (2018九上·洛宁期末) 已知：直角三角形ABC中，∠ACB=90°，CD、CE分别是斜边上的高和中线，AC=CE=10cm，则BD=．

答案解析收藏纠错 + 选题
28. (2018九上·洛宁期末) 直角三角形两锐角平分线相交所成的角的度数为。

答案解析收藏纠错 + 选题
29. (2018九上·洛宁期末) 写一个你喜欢的实数m的值，使得事件“对于二次函数y= $\text{[math]}$ x²﹣（m﹣1）x+3，当x＜﹣3时，y随x的增大而减小”成为随机事件．

答案解析收藏纠错 + 选题
30. (2023·封丘模拟) 如图，管中放置着三根同样的绳子AA₁、BB₁、CC₁ ．小明在左侧选两个打一个结，小红在右侧选两个打一个结，则这三根绳子能连结成一根长绳的概率为．

答案解析收藏纠错 + 选题

三、解答

31. (2018九上·孟津期末) 计算： $\text{[math]}$ .

答案解析收藏纠错 + 选题
32. (2018九上·洛宁期末) 如图，以O为位似中心，将△ABC放大为原来的2倍（不写作法，保留作图痕迹）．

答案解析收藏纠错 + 选题
33. (2018九上·孟津期末) 已知关于x方程2x²﹣（3+4k）x+2k²+k=0，k为何值时，方程有两个不相等的实数根？

答案解析收藏纠错 + 选题
34. (2021九上·瓦房店月考) 如图，某旅游景点要在长、宽分别为20米、12米的矩形水池的正中央建一个与矩形的边互相平行的正方形观赏亭，观赏亭的四角连接四条与矩形的边互相平行且宽度相等的道路，已知道路的宽为正方形边长的 $\text{[math]}$ ，若道路与观赏亭的面积之和是矩形水池面积的 $\text{[math]}$ ，求道路的宽．

答案解析收藏纠错 + 选题
35. (2018九上·孟津期末) 甲、乙、丙三位同学进行足球传球训练，球从一个人脚下随机传到另一个人脚下，且每位传球人传给其余两人的机会是均等的，由甲开始传球，共传三次．
1. （1）求三次传球后，球回到甲脚下的概率；
2. （2）三次传球后，球回到甲脚下的概率大还是传到乙脚下的概率大？
答案解析收藏纠错 + 选题
36. (2018九上·洛宁期末) 如图，已知AB∥CD，AD、BC相交于点E，点F在ED上，且∠CBF=∠D．
1. （1）求证：FB²=FE•FA；
2. （2）若BF=3，EF=2，求△ABE与△BEF的面积之比．
答案解析收藏纠错 + 选题
37. (2018九上·洛宁期末) 已知：如图①，在平行四边形ABCD中，AB=3cm，BC=5cm，AC⊥AB．△ACD沿AC的方向匀速平移得到△PNM，速度为1cm/s；同时，点Q从点C出发，沿着CB方向匀速移动，速度为1cm/s；当△PNM停止平移时，点Q也停止移动，如图②．设移动时间为t（s）（0＜t＜4）．连接PQ、MQ、MC．解答下列问题：
1. （1）当t为何值时，PQ∥AB？
2. （2）当t=3时，求△QMC的面积；
3. （3）是否存在某一时刻t，使PQ⊥MQ？若存在，求出t的值；若不存在，请说明理由
答案解析收藏纠错 + 选题
38. (2018九上·洛宁期末)
1. （1）计算：2sin30°+4cos30°•tan60°﹣cos²45°；
2. （2）抛物线y=ax²+bx+c经过点（0，0），（6，0），且抛物线最高点的纵坐标为3，求这条抛物线的解析式．
答案解析收藏纠错 + 选题
39. (2021·安乡模拟)
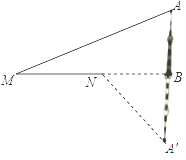
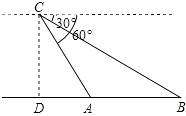
某日，正在我国南海海域作业的一艘大型渔船突然发生险情，相关部门接到求救信号后，立即调遣一架直升飞机和一艘刚在南海巡航的渔政船前往救援．当飞机到达距离海面3000米的高空C处，测得A处渔政船的俯角为60°，测得B处发生险情渔船的俯角为30°，请问：此时渔政船和渔船相距多远？（结果保留根号）

答案解析收藏纠错 + 选题
40. (2018九上·洛宁期末) 第20届世界杯足球赛正在如火如荼的进行，爸爸想通过一个游戏决定小明能否看今晚的比赛：在一个不透明的盒子中放入三张卡片，每张卡片上写着一个实数，分别为3， $\text{[math]}$ ， 2 $\text{[math]}$ （每张卡片除了上面的实数不同以外其余均相同），爸爸让小明从中任意取一张卡片，如果抽到的卡片上的数是有理数，就让小明看比赛，否则就不能看．
1. （1）请你直接写出按照爸爸的规则小明能看比赛的概率；
2. （2）小明想了想，和爸爸重新约定游戏规则：自己从盒子中随机抽取两次，每次抽取一张卡片，第一次抽取后记下卡片上的数，再将卡片放回盒中抽取第二次，如果抽取的两数之积是有理数，自己就看比赛，否则就不看．请你用列表法或树状图法求出按照此规则小明看比赛的概率．
答案解析收藏纠错 + 选题

41. (2018九上·洛宁期末) 为了了解同学们每月零花钱的数额，校园小记者随机调查了本校部分同学，根据调查结果，绘制出了如下两个尚不完整的统计图表．

调查结果统计表

组别	分组 $\text{[math]}$ 单位：元 $\text{[math]}$	人数
A	$\text{[math]}$	4
B	$\text{[math]}$	16
C	$\text{[math]}$	a
D	$\text{[math]}$	b
E	$\text{[math]}$	2

请根据以上图表，解答下列问题：

（1）填空：这次被调查的同学共有人， $\text{[math]}$ ， $\text{[math]}$ ；
（2）求扇形统计图中扇形C的圆心角度数；
（3）该校共有学生1000人，请估计每月零花钱的数额x在 $\text{[math]}$ 范围的人数．

答案解析收藏纠错 + 选题

42. (2018九上·洛宁期末) 在一个口袋里装着白、红、黑三种颜色的小球（除颜色外形状大小完全相同），其中白球3个、红球2个、黑球1个．
1. （1）随机从袋中取出一个球，求取出的球是黑球的概率；
2. （2）若取出的第一只球是红球，不将它放回袋里，从袋中余下的球中再随机地取出1个，这时取出的球是黑球的概率是多少？
3. （3）若取出一个球，将它放回袋中，从袋中再随机地取出一个球，两次取出的球都是白球的概率是多少？（用列表法或树状图计算）
答案解析收藏纠错 + 选题
43. (2018九上·洛宁期末)
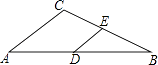
如图，小东在教学楼距地面9米高的窗口C处，测得正前方旗杆顶部A点的仰角为37°，旗杆底部B点的俯角为45°，升旗时，国旗上端悬挂在距地面2.25米处，若国旗随国歌声冉冉升起，并在国歌播放45秒结束时到达旗杆顶端，则国旗应以多少米/秒的速度匀速上升？（参考数据：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75）

答案解析收藏纠错 + 选题
44. (2018九上·洛宁期末) “天天乐”商场销售一种进价为20元/台的台灯，经调查发现，该台灯每天的销售量w（台）与销售单价x（元）满足 $\text{[math]}$ ，设销售这种台灯每天的利润为y（元）.
1. （1）求y与x之间的函数关系式；
2. （2）当销售单价定为多少元时，每天的利润最大？最大利润是多少？
3. （3）在保证销售量尽可能大的前提下，该商场每天还想获得150元的利润，应该将销售单价定为多少元？
答案解析收藏纠错 + 选题
45. (2018九上·洛宁期末) 如图，二次函数 $\text{[math]}$ （a≠0）的图象交x轴于A、B两点，交y轴于点D，点B的坐标为（3，0），顶点C的坐标为（1，4）．
1. （1）求二次函数的解析式和直线BD的解析式；
2. （2）点P是直线BD上的一个动点，过点P作x轴的垂线，交抛物线于点M，当点P在第一象限时，求线段PM长度的最大值；
3. （3）在抛物线上是否存在异于B、D的点Q，使△BDQ中BD边上的高为 $\text{[math]}$ ？若存在求出点Q的坐标；若不存在请说明理由．
答案解析收藏纠错 + 选题