2017年江苏省常州市中考数学模拟试卷（3月份）

更新时间：2024-07-12 浏览次数：568 类型：中考模拟

一、选择题

1. (2017·常州模拟) 在函数y= $\text{[math]}$ 中，自变量x的取值范围是（）

A . x＜2 B . x≤2 C . x＞2 D . x≥2

答案解析收藏纠错 + 选题
2. (2017·靖江模拟) 若一个三角形三个内角度数的比为1：2：3，那么这个三角形最小角的正切值为（　　）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2017·江阴模拟) 如图，在△ABC中，DE∥BC，分别交AB，AC于点D，E．若AD=1，DB=2，则△ADE的面积与△ABC的面积的比等于（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2020九上·常州月考) 如图，AB是半圆的直径，点D是弧AC的中点，∠ABC=50°，则∠DAB等于（）

A . 60° B . 65° C . 70° D . 75°

答案解析收藏纠错 + 选题
5. (2017·常州模拟) 在平面直角坐标系中，以点（2，3）为圆心，2为半径的圆必定（）

A . 与x轴相离，与y轴相切 B . 与x轴，y轴都相离 C . 与x轴相切，与y轴相离 D . 与x轴，y轴都相切

答案解析收藏纠错 + 选题
6. (2017·杭州模拟) 若二次函数y=x²+bx的图象的对称轴是经过点（2，0）且平行于y轴的直线，则关于x的方程x²+bx=5的解为（）

A . x₁=0，x₂=4 B . x₁=1，x₂=5 C . x₁=1，x₂=﹣5 D . x₁=﹣1，x₂=5

答案解析收藏纠错 + 选题
7. (2017·常州模拟)
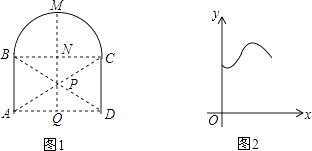
如图1，一个电子蜘蛛从点A出发匀速爬行，它先沿线段AB爬到点B，再沿半圆经过点M爬到点C．如果准备在M、N、P、Q四点中选定一点安装一台记录仪，记录电子蜘蛛爬行的全过程．设电子蜘蛛爬行的时间为x，电子蜘蛛与记录仪之间的距离为y，表示y与x函数关系的图象如图2所示，那么记录仪可能位于图1中的（）

A . 点M B . 点N C . 点P D . 点Q

答案解析收藏纠错 + 选题

二、填空题

8. 已知，在Rt△ABC中，∠C=90°，tanB= $\text{[math]}$ ，则cosA=．

答案解析收藏纠错 + 选题
9. (2017·常州模拟) 反比例函数y= $\text{[math]}$ 的图象经过点（1，6）和（m，﹣3），则m=．

答案解析收藏纠错 + 选题
10. (2017·常州模拟) 某工厂2014年缴税20万元，2016年缴税24万元，这这两年该工厂缴税的年平均增长率为x，根据题意，可得方程为．

答案解析收藏纠错 + 选题
11. (2017·常州模拟) 已知一组数据1，2，x，5的平均数是4，则这组数据的方差是．

答案解析收藏纠错 + 选题
12. (2019·朝阳模拟) 点A（x₁ ， y₁）、B（x₂ ， y₂）在二次函数y=x²﹣4x﹣1的图象上，若当1＜x₁＜2，3＜x₂＜4时，则y₁与y₂的大小关系是y₁y₂ ．（用“＞”、“＜”、“=”填空）

答案解析收藏纠错 + 选题
13. (2017·常州模拟) 已知扇形的圆心角为150°，它所对应的弧长20πcm，则此扇形的半径是 cm．

答案解析收藏纠错 + 选题
14. (2017·常州模拟) 直角坐标系中点A坐标为（5，3），B坐标为（1，0），将点A绕点B逆时针旋转90°得到点C，则点C的坐标为

答案解析收藏纠错 + 选题
15. (2020·济宁模拟) 一次函数y=﹣x+1与反比例函数 $\text{[math]}$ ，x与y的对应值如下表：
x
﹣3
﹣2
﹣1
1
2
3
y=﹣x+1
4
3
2
0
﹣1
﹣2
$\text{[math]}$
$\text{[math]}$
1
2
﹣2
﹣1
﹣ $\text{[math]}$
不等式﹣x+1＞﹣ $\text{[math]}$ 的解为．

答案解析收藏纠错 + 选题
16. (2017·常州模拟) 如图，△ABC的三个顶点的坐标分别为A（﹣3，5），B（﹣3，0），C（2，0），将△ABC绕点B顺时针旋转一定角度后使A落在y轴上，与此同时顶点C恰好落在y= $\text{[math]}$ 的图象上，则k的值为．

答案解析收藏纠错 + 选题
17. (2018九上·东台期末) 如图，在平面直角坐标系中，已知点A（0，1）、点B（0，1+t）、C（0，1﹣t）（t＞0），点P在以D（3，3）为圆心，1为半径的圆上运动，且始终满足∠BPC=90°，则t的最小值是．

答案解析收藏纠错 + 选题

三、解答题

18. (2017·常州模拟) 化简：
1. （1） $\text{[math]}$ ﹣tan45°+sin²45°
2. （2） |﹣ $\text{[math]}$ |+ $\text{[math]}$ ﹣sin30°+（π+3）⁰ ．
答案解析收藏纠错 + 选题
19. (2017·常州模拟) 解方程：
1. （1）（4x﹣1）²﹣9=0
2. （2） 3（x﹣2）²=2﹣x．
答案解析收藏纠错 + 选题
20. (2017·常州模拟) 某区对即将参加中考的5000名初中毕业生进行了一次视力抽样调查，绘制出频数分布表和频数分布直方图的一部分．
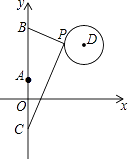
请根据图表信息回答下列问题：
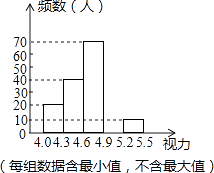
视力
频数（人）
频率
4.0≤x＜4.3
20
0.1
4.3≤x＜4.6
40
0.2
4.6≤x＜4.9
70
0.35
4.9≤x＜5.2
a
0.3
5.2≤x＜5.5
10
b
1. （1）本次调查的样本为，样本容量为；
2. （2）在频数分布表中，a=，b=，并将频数分布直方图补充完整；
3. （3）若视力在4.6以上（含4.6）均属正常，根据上述信息估计全区初中毕业生中视力正常的学生有多少人？
答案解析收藏纠错 + 选题
21. (2020·常州模拟) 甲、乙、丙三位同学用质地、大小完全一样的纸片分别制作一张卡片a、b、c，收集后放在一个不透明的箱子中，然后每人从箱子中随机抽取一张．
1. （1）用列表或画树状图的方法表示三位同学抽到卡片的所有可能的结果；
2. （2）求三位同学中至少有一人抽到自己制作卡片的概率．
答案解析收藏纠错 + 选题
22. (2017·常州模拟) 如图，方格纸中的每个小方格都是边长为1的正方形，我们把以格点间连线为边的三角形称为“格点三角形”，图中的△ABC就是格点三角形，建立如图所示的平面直角坐标系，点C的坐标为（0，﹣1）．
1. （1）在如图的方格纸中把△ABC以点O为位似中心扩大，使放大前后的位似比为1：2，画出△A₁B₂C₂（△ABC与△A₁B₂C₂在位似中心O点的两侧，A，B，C的对应点分别是A₁ ， B₂ ， C₂）．
2. （2）利用方格纸标出△A₁B₂C₂外接圆的圆心P，P点坐标是，⊙P的半径=．（保留根号）
答案解析收藏纠错 + 选题
23. (2017·常州模拟) 已知：如图，等腰△ABC中，AB=BC，AE⊥BC于E，EF⊥AB于F，若CE=2，cos∠AEF= $\text{[math]}$ ，求BE的长．

答案解析收藏纠错 + 选题
24. (2017·常州模拟) 如图，轮船甲位于码头O的正西方向A处，轮船乙位于码头O的正北方向C处，测得∠CAO=45°，轮船甲自西向东匀速行驶，同时轮船乙沿正北方向匀速行驶，它们的速度分别为45km/h和36km/h，经过0.1h，轮船甲行驶至B处，轮船乙行驶至D处，测得∠DBO=58°，此时B处距离码头O多远？（参考数据：sin58°≈0.85，cos58°≈0.53，tan58°≈1.60）

答案解析收藏纠错 + 选题
25. (2017·常州模拟) 旅游公司在景区内配置了50辆观光车供游客租赁使用，假定每辆观光车一天内最多只能出租一次，且每辆车的日租金是x（元）．发现每天的营运规律如下：当x不超过100元时，观光车能全部租出；当x超过100元时，每辆车的日租金每增加5元，租出去的观光车就会减少1辆．已知所有观光车每天的管理费是1100元．当每辆车的日租金为多少元时，每天的净收入最多？（注：净收入=租车收入﹣管理费）

答案解析收藏纠错 + 选题
26. (2017·常州模拟)
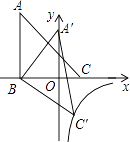
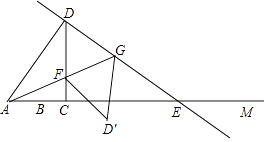
如图，射线AM上有一点B，AB=6，点C是射线AM上异于B的一点，过C作CD⊥AM，且CD= $\text{[math]}$ AC，过D点作DE⊥AD，交射线AM于E，在射线CD取点F，使得CF=CB，连接AF并延长，交DE于点G，设AC=3x．
1. （1）当C在B点右侧时，求AD．DF的长．（用关于x的代数式表示）
2. （2）当x为何值时，△AFD是等腰三角形；
3. （3）作点D关于AG的对称点D′，连接FD′，GD′，若四边形DFD′G是平行四边形，求x的值．（直接写出答案）
答案解析收藏纠错 + 选题
27. (2017·常州模拟)
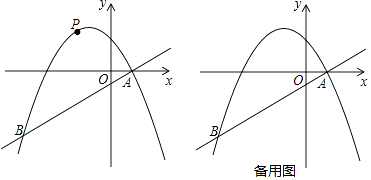
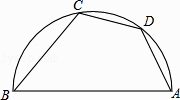
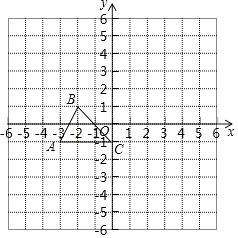
如图，在平面直角坐标系中，直线y= $\text{[math]}$ x﹣1与抛物线y=﹣ $\text{[math]}$ x²+bx+c交于A，B两点，点A在x轴上，点B的横坐标为﹣8，点P是直线AB上方的抛物线上的一动点（不与点A，B重合）．
1. （1）求该抛物线的函数关系式；
2. （2）连接PA、PB，在点P运动过程中，是否存在某一位置，使△PAB恰好是一个以点P为直角顶点的等腰直角三角形，若存在，求出点P的坐标；若不存在，请说明理由；
3. （3）过P作PD∥y轴交直线AB于点D，以PD为直径作⊙E，求⊙E在直线AB上截得的线段的最大长度．
答案解析收藏纠错 + 选题