北京市朝阳区2019年中考数学二模考试试卷

更新时间：2024-07-13 浏览次数：283 类型：中考模拟

一、选择题（共8小题）

1. (2019·朝阳模拟) 下列轴对称图形中只有一条对称轴的是（　　）

A . B . C . D .

答案解析收藏纠错 + 选题
2. (2019·朝阳模拟) 2019年4月25﹣27日，第二届“一带一路”国际合作高峰论坛在北京举行，自“一带一路”倡议提出以来，五年之间，北京市对外贸易总额累计约30000亿美元，年均增速1.5%．将30000用科学记数法表示应为（　　）

A . 3.0×10³ B . 0.3×10⁴ C . 3.0×10⁴ D . 0.3×10⁵

答案解析收藏纠错 + 选题
3. (2019·朝阳模拟) 如图是某个几何体的展开图，该几何体是（　　）

A . 圆锥 B . 圆柱 C . 三棱柱 D . 四棱柱

答案解析收藏纠错 + 选题
4. (2019·朝阳模拟) 实数a，b，c，d在数轴上的对应点的位置如图所示，则正确结论是（　　）

A . ac＞0 B . |b|＜|c| C . a＞﹣d D . b+d＞0

答案解析收藏纠错 + 选题
5. (2019·朝阳模拟) 如图，直线l₁∥l₂ ， AB＝BC，CD⊥AB于点D，若∠DCA＝20°，则∠1的度数为（　　）

A . 80° B . 70° C . 60° D . 50°

答案解析收藏纠错 + 选题
6. (2019·朝阳模拟) 如果x﹣3y＝0，那么代数式 $\text{[math]}$ 的值为（　　）

A . ﹣2 B . 2 C . $\text{[math]}$ D . 3

答案解析收藏纠错 + 选题
7. (2020·蠡县模拟) 某公司生产的一种产品按照质量由高到低分为A，B，C，D四级，为了增加产量、提高质量，该公司改进了一次生产工艺，使得生产总量增加了一倍．为了解新生产工艺的效果，对改进生产工艺前、后的四级产品的占比情况进行了统计，绘制了如下扇形图：

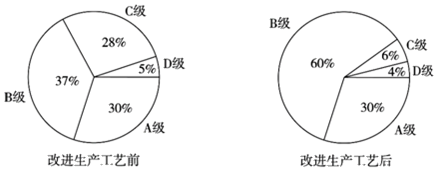
根据以上信息，下列推断合理的是（　　）

A . 改进生产工艺后，A级产品的数量没有变化 B . 改进生产工艺后，B级产品的数量增加了不到一倍 C . 改进生产工艺后，C级产品的数量减少 D . 改进生产工艺后，D级产品的数量减少

答案解析收藏纠错 + 选题
8. (2020八下·越城期末) 小明使用图形计算器探究函数y＝ $\text{[math]}$ 的图象，他输入了一组a，b的值，得到了下面的函数图象，由学习函数的经验，可以推断出小明输入的a，b的值满足（　　）

A . a＞0，b＞0 B . a＞0，b＜0 C . a＜0，b＞0 D . a＜0，b＜0

答案解析收藏纠错 + 选题

二、填空题（共8小题）

9. (2020·西宁模拟) 函数y＝ $\text{[math]}$ 中，自变量x的取值范围是．

答案解析收藏纠错 + 选题
10. (2019七下·北京期末) 颐和园坐落在北京西郊，是第一批全国重点文物保护单位之一．小万去颐和园参加实践活动时发现有的窗户造型是正八边形，如下图所示，则∠1＝°．

答案解析收藏纠错 + 选题
11. (2019·朝阳模拟) 点A（x₁ ， y₁）、B（x₂ ， y₂）在二次函数y=x²﹣4x﹣1的图象上，若当1＜x₁＜2，3＜x₂＜4时，则y₁与y₂的大小关系是y₁y₂ ．（用“＞”、“＜”、“=”填空）

答案解析收藏纠错 + 选题

12. (2019·朝阳模拟) 水果在物流运输过程中会产生一定的损耗，下表统计了某种水果发货时的重量和收货时的重量．

发货时重量（kg）	100	200	300	400	500	600	1000
收货时重量（kg）	94	187	282	338	435	530	901

若一家水果商店以6元/kg的价格购买了5000kg该种水果，不考虑其他因素，要想获得约15000元的利润，销售此批水果时定价应为元/kg．

答案解析收藏纠错 + 选题

13. (2019·朝阳模拟) 如图，AB是⊙O的直径，C是⊙O上一点，将 $\text{[math]}$ 沿直线AC翻折，若翻折后的图形恰好经过点O，则∠CAB＝°．

答案解析收藏纠错 + 选题
14. (2021·海安模拟) 如图，在正方形ABCD中，对角线AC，BD相交于点O，E是OB的中点，连接AE并延长交BC于点F．若△BEF的面积为1，则△AED的面积为．

答案解析收藏纠错 + 选题

15. (2019·朝阳模拟) 世界上大部分国家都使用摄氏温度（℃），但美、英等国的天气预报仍然使用华氏温度（℉），两种计量之间有如下的对应表：

摄氏温度（℃）	0	10	20	30	40	50
华氏温度（℉）	32	50	68	86	104	122

由上表可以推断出，华氏0度对应的摄氏温度是℃，若某一温度时华氏温度的值与对应的摄氏温度的值相等，则此温度为℃．

答案解析收藏纠错 + 选题

16. (2019·朝阳模拟) 某公园门票的收费标准如下：

门票类别

成人票

儿童票

团体票（限5张及以上）

价格（元/人）

100

40

60

有两个家庭分别去该公园游玩，每个家庭都有5名成员，且他们都选择了最省钱的方案购买门票，结果一家比另一家少花40元，则花费较少的一家花了元．

答案解析收藏纠错 + 选题

三、解答题（共12小题）

17. (2023九上·费县期末) 计算： $\text{[math]}$ ．

答案解析收藏纠错 + 选题
18. (2019·朝阳模拟) 解不等式组 $\text{[math]}$ 并写出它的所有整数解．

答案解析收藏纠错 + 选题
19. (2020·河池模拟) 下面是小东设计的“过直线上一点作这条直线的垂线”的尺规作图过程．
已知：直线l及直线l上一点P．

求作：直线PQ，使得PQ⊥l．

作法：如图，

①在直线l上取一点A（不与点P重合），分别以点P，A为圆心，AP长为半径画弧，两弧在直线l的上方相交于点B；

②作射线AB，以点B为圆心，AP长为半径画弧，交AB的延长线于点Q；

③作直线PQ．

所以直线PQ就是所求作的直线．

根据小东设计的尺规作图过程，
1. （1）使用直尺和圆规，补全图形；（保留作图痕迹）
2. （2）完成下面的证明．
  证明：连接BP，
  
  ∵＝＝＝AP，
  
  ∴点A，P，Q在以点B为圆心，AP长为半径的圆上．
  
  ∴∠APQ＝90°（）．（填写推理的依据）
  
  即PQ⊥l．
答案解析收藏纠错 + 选题
20. (2019·朝阳模拟) 关于x的方程mx²﹣2mx+m+n＝0有两个实数根．
1. （1）求实数m，n需满足的条件；
2. （2）写出一组满足条件的m，n的值，并求此时方程的根．
答案解析收藏纠错 + 选题
21. (2019·朝阳模拟) 如图，在▱ABCD中，∠ABD＝90°，延长AB至点E，使BE＝AB，连接CE．
1. （1）求证：四边形BECD是矩形；
2. （2）连接DE交BC于点F，连接AF，若CE＝2，∠DAB＝30°，求AF的长．
答案解析收藏纠错 + 选题
22. (2019·朝阳模拟) 如图，△ABC内接于以AB为直径的⊙O，过点A作⊙O的切线，与BC的延长线相交于点D，在CB上截取CE＝CD，连接AE并延长，交⊙O于点F，连接CF．
1. （1）求证：AC＝CF；
2. （2）若AB＝4，sinB＝ $\text{[math]}$ ，求EF的长．
答案解析收藏纠错 + 选题
23. (2019·朝阳模拟) 在平面直角坐标系xOy中，反比例函数y＝ $\text{[math]}$ 的图象经过点P（3，4）．
1. （1）求k的值；
2. （2）求OP的长；
3. （3）直线y＝mx（m≠0）与反比例函数的图象有两个交点A，B，若AB＞10，直接写出m的取值范围．
答案解析收藏纠错 + 选题
24. (2019·朝阳模拟) 如图，P是半圆O中 $\text{[math]}$ 所对弦AB上一动点，过点P作PM⊥AB交 $\text{[math]}$ 于点M，作射线PN交 $\text{[math]}$ 于点N，使得∠NPB＝45°，连接MN．已知AB＝6cm，设A，P两点间的距离为xcm，M，N两点间的距离为ycm．（当点P与点A重合时，点M也与点A重合，当点P与点B重合时，y的值为0）

小超根据学习函数的经验，对函数y随自变量x的变化而变化的规律进行了探究．

下面是小超的探究过程，请补充完整：
1. （1）按照下表中自变量x的值进行取点、画图、测量，得到了y与x的几组对应值；
  
  x/cm
  
  0
  
  1
  
  2
  
  3
  
  4
  
  5
  
  6
  
  y/cm
  
  4.2
  
  2.9
  
  2.6
  
  2.0
  
  1.6
  
  0
  
  （说明：补全表格时相关数值保留一位小数）
2. （2）建立平面直角坐标系，描出以补全后的表中各对对应值为坐标的点，画出该函数的图象；
3. （3）结合画出的函数图象，解决问题：当MN＝2AP时，AP的长度约为cm．
答案解析收藏纠错 + 选题

25. (2019·朝阳模拟) 某部门为新的生产线研发了一款机器人，为了了解它的操作技能情况，在相同条件下与人工操作进行了抽样对比．过程如下，请补充完整．

收集数据对同一个生产动作，机器人和人工各操作20次，测试成绩（十分制）如下：

机器人	8.0	8.1	8.1	8.1	8.2	8.2	8.3	8.4	8.4	9.0
	9.0	9.0	9.1	9.1	9.4	9.5	9.5	9.5	9.5	9.6

人工	6.1	6.2	6.6	7.2	7.2	7.5	8.0	8.2	8.3	8.5
	9.1	9.6	9.8	9.9	9.9	9.9	10	10	10	10

整理、描述数据按如下分段整理、描述这两组样本数据：

成绩x

人数

生产方式

6≤x＜7

7≤x＜8

8≤x＜9

9≤x≤10

机器人

人工

（说明：成绩在9.0分及以上为操作技能优秀，8.0～8.9分为操作技能良好，6.0～7.9分为操作技能合格，6.0分以下为操作技能不合格）

分析数据两组样本数据的平均数、中位数、众数和方差如下表所示：

	平均数	中位数	众数	方差
机器人	8.8		9.5	0.333
人工	8.6		10	1.868

得出结论

（1）如果生产出一个产品，需要完成同样的操作200次，估计机器人生产这个产品达到操作技能优秀的次数为；
（2）请结合数据分析机器人和人工在操作技能方面各自的优势：．

答案解析收藏纠错 + 选题

26. (2019·朝阳模拟) 在平面直角坐标系xOy中，抛物线y＝ax²﹣2a²x（a≠0）的对称轴与x轴交于点P．
1. （1）求点P的坐标（用含a的代数式表示）；
2. （2）记函数 $\text{[math]}$ （﹣1≤x≤3）的图象为图形M，若抛物线与图形M恰有一个公共点，结合函数的图象，求a的取值范围．
答案解析收藏纠错 + 选题
27. (2019·朝阳模拟) ∠MON＝45°，点P在射线OM上，点A，B在射线ON上（点B与点O在点A的两侧），且AB＝1，以点P为旋转中心，将线段AB逆时针旋转90°，得到线段CD（点C与点A对应，点D与点B对应）．
1. （1）如图，若OA＝1，OP＝ $\text{[math]}$ ，依题意补全图形；
2. （2）若OP＝ $\text{[math]}$ ，当线段AB在射线ON上运动时，线段CD与射线OM有公共点，求OA的取值范围；
3. （3）一条线段上所有的点都在一个圆的圆内或圆上，称这个圆为这条线段的覆盖圆．若OA＝1，当点P在射线OM上运动时，以射线OM上一点Q为圆心作线段CD的覆盖圆，直接写出当线段CD的覆盖圆的直径取得最小值时OP和OQ的长度．
答案解析收藏纠错 + 选题
28. (2019·朝阳模拟) M（﹣1，﹣ $\text{[math]}$ ），N（1，﹣ $\text{[math]}$ ）是平面直角坐标系xOy中的两点，若平面内直线MN上方的点P满足：45°≤∠MPN≤90°，则称点P为线段MN的可视点．
1. （1）在点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，A₄（2，2）中，线段MN的可视点为；
2. （2）若点B是直线y＝x+ $\text{[math]}$ 上线段MN的可视点，求点B的横坐标t的取值范围；
3. （3）直线y＝x+b（b≠0）与x轴交于点C，与y轴交于点D，若线段CD上存在线段MN的可视点，直接写出b的取值范围．
答案解析收藏纠错 + 选题