2018-2019学年初中数学浙教版七年级下册4.3 用乘法...

更新时间：2019-02-27 浏览次数：310 类型：同步测试

一、单选题

1. (2018七上·大庆期中) 整式x²+kx+25为某完全平方式展开后的结果，则k的值为（）

A . 5 B . ±5 C . 10 D . ±10

答案解析收藏纠错 + 选题
2. a是有理数，则多项式﹣a²+a﹣ $\text{[math]}$ 的值（）

A . 一定是正数 B . 一定是负数 C . 不可能是正数 D . 不可能是负数

答案解析收藏纠错 + 选题
3. (2019八上·兴仁期末) 下列因式分解结果正确的是（）．

A . B . C . D .

答案解析收藏纠错 + 选题
4. (2024七下·田阳期中) 因式分解x﹣4x³的最后结果是（）

A . x（1﹣2x）² B . x（2x﹣1）（2x+1） C . x（1﹣2x）（2x+1） D . x（1﹣4x²）

答案解析收藏纠错 + 选题
5. 若x﹣y+3=0，则x（x﹣4y）+y（2x+y）的值为（）

A . 9 B . ﹣9 C . 3 D . ﹣3

答案解析收藏纠错 + 选题
6. 下列各式中，不能用完全平方公式分解的个数为（）
①x²﹣10x+25；②4a²+4a﹣1；③x²﹣2x﹣1；④ $\text{[math]}$ ；⑤ $\text{[math]}$ ．

A . 1个 B . 2个 C . 3个 D . 4个

答案解析收藏纠错 + 选题
7. 计算105²－95²的结果为（）

A . 1000 B . 1980 C . 2000 D . 4000

答案解析收藏纠错 + 选题
8. 将下列多项式分解因式，结果中不含因式x-1的是（）

A . x²-1 B . x(x-2)+(2-x) C . x²-2x+1 D . x²+2x+1

答案解析收藏纠错 + 选题
9. (2020八下·张掖期末) 下列各多项式中，不能用平方差公式分解的是（）.

A . a²b²－1 B . 4－0.25a² C . －a²－b² D . －x²+1

答案解析收藏纠错 + 选题
10. (2018八上·双清月考) 小明在抄分解因式的题目时，不小心漏抄了x的指数，他只知道该数为不大于10的正整数，并且能利用平方差公式分解因式，他抄在作业本上的式子是x^□﹣4y²（“□”表示漏抄的指数），则这个指数可能的结果共有（）

A . 2种 B . 3种 C . 4种 D . 5种

答案解析收藏纠错 + 选题

二、填空题

11. 已知二次三项式x²+mx+9能用完全平方公式分解因式，则m的值为．

答案解析收藏纠错 + 选题
12. (2021·常州模拟) 分解因式： $\text{[math]}$ =

答案解析收藏纠错 + 选题
13. (2020九下·复兴月考) 若a，b互为相反数，则a²﹣b²=．

答案解析收藏纠错 + 选题
14. (2018八上·天台月考) 在日常生活中，如取款、上网需要密码，有一种因式分解法产生密码，例如x⁴－y⁴＝(x－y)(x＋y)(x²＋y²)，当x＝9，y＝9时，x－y＝0，x＋y＝18，x²＋y²＝162，则密码018162. 对于多项式4x³－xy² ，取x＝10，y＝10，用上述方法产生密码是(写出一个即可).

答案解析收藏纠错 + 选题

三、解答题

15. (2018八下·深圳期中) 分解因式
1. （1） 4a²-8ab+4b²
2. （2） x²（m﹣n）﹣y²（m﹣n）
答案解析收藏纠错 + 选题
16. 把下列各式因式分解:
1. （1） (2a-b)²+8ab;
2. （2） (x²-1)²-6(x²-1)+9;
3. （3） (m²-4m)²+8(m²-4m)+16.
答案解析收藏纠错 + 选题
17. 请你说明：m（m+1）（m+2）（m+3）+1是一个完全平方式．

答案解析收藏纠错 + 选题
18. 解答题
1. （1）根据如图所示的图形写出一个恒等代数式；
2. （2）已知x- $\text{[math]}$ =3(其中x>0)，求x+ $\text{[math]}$ 的值.
答案解析收藏纠错 + 选题
19. (2017七下·常州期中)
教材中，在计算如图1所示的正方形ABCD的面积时，分别从两个不同的角度进行了操作：

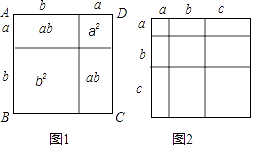
（i）把它看成是一个大正方形，则它的面积为（a+b）²；

（ii）把它看成是2个小长方形和2个小正方形组成的，则它的面积为a²+2ab+b²；因此，可得到等式：（a+b）²=a²+2ab+b² ．
1. （1）类比教材中的方法，由图2中的大正方形可得等式：．
2. （2）
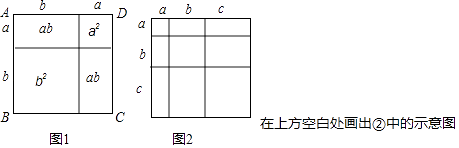
  试在图2右边空白处画出面积为2a²+3ab+b²的长方形的示意图（标注好a，b），由图形可知，多项式2a²+3ab+b²可分解因式为：．
3. （3）若将代数式（a₁+a₂+a₃+…+a₂₀）²展开后合并同类项，得到多项式N，则多项式N的项数一共有项．
答案解析收藏纠错 + 选题
20. (2019八上·澄海期末) 下面是某同学对多项式 $\text{[math]}$ 进行因式分解的过程．
解：设 $\text{[math]}$ ，则

原式= $\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$
1. （1）该同学因式分解的结果是否彻底？（填“彻底”或“不彻底”）．若不彻底，请直接写出因式分解的最后结果．
2. （2）请你模仿以上方法尝试对多项式 $\text{[math]}$ 进行因式分解．
答案解析收藏纠错 + 选题
21. (2018八上·长春期末) 阅读下列材料：
“a²≥0”这个结论在数学中非常有用，有时我们需要将代数式配成完全平方式．例如：x²＋4x＋5＝x²＋4x＋4＋1＝（x＋2）²＋1，
∵（x＋2）²≥0， ∴（x＋2）²＋1≥1， ∴x²＋4x＋5≥1.
试利用“配方法”解决下列问题：
1. （1）填空：x²-4x＋5＝(x)²＋；
2. （2）已知，x²-4x＋y²＋2y＋5＝0，求x＋y的值；
3. （3）比较代数式x²-1与2x-3的大小．（提示：比差法）
答案解析收藏纠错 + 选题
22. (2018八上·黔南期末) 先阅读下列材料：
我们已经学过将一个多项式分解因式的方泫有提公因式法和运用公式法，其实分解因式的方法还有分组分解法、拆项法、十字相乘法等等．
①分组分解法：将一个多项式适当分组后，可提公因式或运用公式继续分解的方法．
如： $\text{[math]}$ ，                    $\text{[math]}$
分组分解法：
解：原式 $\text{[math]}$           解：原式 $\text{[math]}$
$\text{[math]}$                         $\text{[math]}$
$\text{[math]}$
②拆项法：将一个多项式的某一项拆成两项后，可提公因式或运用公式继续分解的方法．
如： $\text{[math]}$
解：原式 $\text{[math]}$
$\text{[math]}$
$\text{[math]}$
$\text{[math]}$
请你仿照以上方法，探索并解决下列问题：
1. （1）分解因式： $\text{[math]}$ ；
2. （2）分解因式： $\text{[math]}$ .
答案解析收藏纠错 + 选题