苏州市立达中学2016-2017学年八年级下学期期中考试试卷

杨伯伯家小院子的四棵小树E、F、G、H刚好在其梯形院子ABCD各边的中点上，若在四边形EFGH地上种小草，则这块草地的形状是（ ）

如图，以正方形ABCD的一边向形外作等边△ABE，BD与EC交于点F，则∠AFD等于（ ）

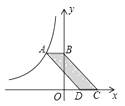
如图，将矩形ABCD分成15个大小相等的正方形，E、F、G、H分别在AD、AB、BC、CD边上，且都是某个小正方形的顶点，若四边形EFGH的面积为1，则矩形ABCD的面积为（ ）

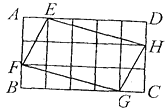
如图，在▱ABCD中，AD=2AB，F是AD的中点，作CE⊥AB，垂足E在线段AB上，连接EF、CF，则下列结论中一定成立的是（ ） ．

①∠DCF=∠BCD；②EF=CF；③S_△BEC ＝2S_△CEF；④∠DFE=3∠AEF．

将一块直角三角形纸片ABC折叠，使点A与点C重合，展开后平铺在桌面上(如图所示)． 若∠C＝90°，BC＝8cm，则折痕DE的长度是cm．

已知如图：▱ABCD中，AD=8，AB=6，DE平分∠ADC交BC于E，则BE= ．

如图，在菱形ABCD中，对角线AC与BD相交于点O，OE⊥AB，垂足为E点，若∠ADC=130°，

则∠AOE=．

如图，正比例函数y＝x与反比例函数y＝ 的图像交于点A、点C，AB⊥x轴于点B，CD⊥x轴于点D，则四边形ABCD的面积为．

如图▱ABCD中，E、F分别在CD和BC的延长线上，AE//BD，EF⊥BC，EF=3，CF=1，则AB的长是．

如图，边长为1的菱形ABCD中，∠DAB=60°，连接对角线AC，以AC为边作第二个菱形ACEF，使∠FAC=60°，连接AE，再以AE为边作第三个菱形AEGH，使∠HAE=60°，按此规律下去，则第n个菱形的边长为．

作图题：如图，正方形网格中的每个小正方形的边长都是1，每个小正方形的顶点叫做格点．△AOB的三个顶点A，O，B都在格点上．

为了了解学生平均每天“诵读经典”的时间，在全校范围内随机抽查了部分学生进行调查统计，并将调查统计的结果分为：每天诵读时间t≤20分钟的学生记为A类，20分钟＜t≤40分钟的学生记为B类，40分钟＜t≤60分钟的学生记为C类，t＞60分钟的学生记为D类四种．将收集的数据绘制成如下两幅不完整的统计图．请根据图中提供的信息，解答下列问题：

如图，一次函数 的图象与反比例函数 的图象交于点A﹙−2，−5﹚、

C﹙5，n﹚，交y轴于点B，交x轴于点D．

如图，在△ABC中，D是BC边的中点，E、F分别在AD及其延长线上，CE∥BF，连结BE、CF．

在△ABC中，∠BAC＝90°，AB＝AC点D为直线BC上一动点(点D不与B、C重合) ．以AD为边作正方形ADEF，连接CF．

已知，如图四边形AOBC为正方形，点C的坐标为(4 ，0)，动点P沿着折线OACB的方向以1个单位每秒的速度匀速运动，同时点Q沿着折线OBCA的方向匀速运动，速度是2个单位长度每秒，运动时间为t秒，当他们相遇时同时停止运动．