浙江省温州市苍南县2018届数学中考一模试卷

更新时间：2024-07-13 浏览次数：562 类型：中考模拟

一、单选题

1. (2018·苍南模拟) 在 $\text{[math]}$ ， $\text{[math]}$ ，0，－2这四个数中，为无理数的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . 0 D . －2

答案解析收藏纠错 + 选题
2. (2018·苍南模拟) 下列计算正确的是（）

A . a²+a³=a⁵ B . a²•a³=a⁵ C . （2a）²=4a D . （a²）³=a⁵

答案解析收藏纠错 + 选题
3. (2018·苍南模拟) 如图所示，该圆柱体的左视图是（）

A . B . C . D .

答案解析收藏纠错 + 选题
4. (2018·苍南模拟) 如图，△ABC内接于⊙O，∠A=68°，则∠OBC等于（）

A . 22° B . 26° C . 32° D . 34°

答案解析收藏纠错 + 选题
5. (2023·中山模拟) 某校数学兴趣小组在一次数学课外活动中，随机抽查该校10名同学参加今年初中学业水平考试的体育成绩，统计结果如下表所示：

成绩（分）

36

37

38

39

40

人数（人）

1

2

1

4

2

表中表示成绩分数的数据中，中位数是（）

A . 38分 B . 38.5分 C . 39分 D . 39.5分

答案解析收藏纠错 + 选题
6. (2018九上·封开期中) 用配方法解一元二次方程x²﹣6x﹣10=0时，下列变形正确的为（）

A . （x+3）²=1 B . （x﹣3）²=1 C . （x+3）²=19 D . （x﹣3）²=19

答案解析收藏纠错 + 选题
7. (2018·苍南模拟) 不等式组 $\text{[math]}$ 的解集是（）

A . x≥2 B . 1＜x＜2 C . 1＜x≤2 D . x≤2

答案解析收藏纠错 + 选题
8. (2018·苍南模拟) 已知点（﹣2，y₁），（1，0），（3，y₂）都在一次函数y=kx﹣2的图象上，则y₁ ， y₂ ， 0的大小关系是（）

A . 0＜y₁＜y₂ B . y₁＜0＜y₂ C . y₁＜y₂＜0 D . y₂＜0＜y₁

答案解析收藏纠错 + 选题
9. (2018·苍南模拟) 七巧板是我们祖先的一项卓越创造，被誉为“东方魔板”．如图是一个七巧板迷宫，它恰好拼成了一个正方形ABCD，其中点E，P分别是AD，CD的中点，AB=2 $\text{[math]}$ ，一只蚂蚁从A处沿图中实线爬行到出口P处，则它爬行的最短路径长为（）

A . 3 B . 2+ C . 4 D . 3

答案解析收藏纠错 + 选题
10. (2021·黄冈模拟) 如图，矩形ABCD中，AB=8，BC=6，将矩形ABCD绕点A逆时针旋转得到矩形AEFG，AE，FG分别交射线CD于点PH，连结AH，若P是CH的中点，则△APH的周长为（）

A . 15 B . 18 C . 20 D . 24

答案解析收藏纠错 + 选题

二、填空题

11. (2019·宁波模拟) 分解因式：a²﹣4a=．

答案解析收藏纠错 + 选题
12. (2018·苍南模拟) 一个布袋里装有10个只有颜色不同的球，这10个球中有m个红球，从布袋中摸出一个球，记下颜色后放回，搅匀，再摸出一个球，通过大量重复试验后发现，摸到红球的频率稳定在0.3左右，则m的值约为．

答案解析收藏纠错 + 选题
13. (2023八下·瑶海期中) 某种品牌手机经过4，5月份连续两次降价，每部售价由5000降到3600元，且5月份降价的百分率是4月份降价的百分率的2倍．设4月份降价的百分率为x，根据题意可列方程：（不解方程）．

答案解析收藏纠错 + 选题
14. (2018·苍南模拟) 如图，把菱形ABCD沿折痕AH翻折，使B点落在BC延长线上的点E处，连结DE，若∠B=30°，则∠CDE=°．

答案解析收藏纠错 + 选题
15. (2018·苍南模拟) 如图，要在宽AB为20米的瓯海大道两边安装路灯，路灯的灯臂CD与灯柱BC成120°角，灯罩的轴线DO与灯臂CD垂直，当灯罩的轴线DO通过公路路面的中心线（即O为AB的中点）时照明效果最佳，若CD= $\text{[math]}$ 米，则路灯的灯柱BC高度应该设计为米（计算结果保留根号）．

答案解析收藏纠错 + 选题
16. (2018·苍南模拟) 如图，直角坐标系xOy中，直线y=﹣x+b分别交x，y轴的正半轴于点A，B，交反比例函数y=﹣ $\text{[math]}$ 的图象于点C，D（点C在第二象限内），过点C作CE⊥x轴于点E，记四边形OBCE的面积为S₁ ， △OBD的面积为S₂ ，若 $\text{[math]}$ ，则CD的长为．

答案解析收藏纠错 + 选题

三、解答题

17. (2018·苍南模拟) 计算：（﹣2）⁰﹣（ $\text{[math]}$ ）²+|﹣1|．

答案解析收藏纠错 + 选题
18. (2018·苍南模拟) 如图，在△ABE中，C为边AB延长线上一点，BC=AE，点D在∠EBC内部，且∠EBD=∠A=∠DCB．
1. （1）求证：△ABE≌△CDB．
2. （2）连结DE，若∠CDB=60°，∠AEB=50°，求∠BDE的度数．
答案解析收藏纠错 + 选题
19. (2018·苍南模拟) 如图，5×5的正方形网格中隐去了一些网格线，AB，CD间的距离是2个单位，CD，EF间的距离是3个单位，格点O在CD上（网格线的交点叫格点）．请分别在图①、②中作格点三角形OPQ，使得∠POQ=90°，其中点P在AB上，点Q在EF上，且它们不全等．

答案解析收藏纠错 + 选题
20. (2018·苍南模拟) 随着道路交通的不断完善，某市旅游业快速发展，该市旅游景区有A、B、C、D、E等著名景点，市旅游部门统计绘制出2017年“五•一”长假期间旅游情况统计图（不完整）如下所示，根据相关信息解答下列问题：
1. （1） 2017年“五•一”期间，该市旅游景点共接待游客万人，扇形统计图中A景点所对应的圆心角的度数是，并补全条形统计图．
2. （2）在等可能性的情况下，甲、乙两个旅行团在A、B、D三个景点中选择去同一景点的概率是多少？请用画树状图或列表加以说明．
答案解析收藏纠错 + 选题
21. (2019·沈丘模拟) 如图，钝角△ABC中，AB=AC，BC=2 $\text{[math]}$ ，O是边AB上一点，以O为圆心，OB为半径作⊙O，交边AB于点D，交边BC于点E，过E作⊙O的切线交边AC于点F．
1. （1）求证：EF⊥AC．
2. （2）连结DF，若∠ABC=30°，且DF∥BC，求⊙O的半径长．
答案解析收藏纠错 + 选题
22. (2018·苍南模拟) 如图，▱ABCD位于直角坐标系中，AB=2，点D（0，1），以点C为顶点的抛物线y=ax²+bx+c经过x轴正半轴上的点A，B，CE⊥x轴于点E．
1. （1）求点A，B，C的坐标．
2. （2）将该抛物线向上平移m个单位恰好经过点D，且这时新抛物线交x轴于点M，N．
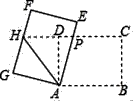
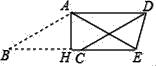
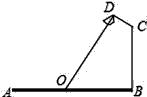
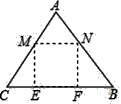
  ①求MN的长．
  
  ②点P是新抛物线对称轴上一动点，将线段AP绕点A顺时针旋转60°得AQ，则OQ的最小值为（直接写出答案即可）
答案解析收藏纠错 + 选题
23. (2018·苍南模拟) 如图，王爷爷家院子里有一块三角形田地ABC，AB=AC=5米，BC=6米，现打算把它开垦出一个矩形MNFE区域种植韭菜，△AMN区域种植芹菜，△CME和△BNF区域种植青菜（开垦土地面积损耗均忽略不计），其中点M，N分别在AC，AB上，点E，F在BC上，已知韭菜每平方米收益100元，芹菜每平方米收益60元，青菜每平方米收益40元，设CM=5x米，王爷爷的蔬菜总收益为W元．
1. （1）当矩形MNFE恰好为正方形时，求韭菜种植区域矩形MNFE的面积．
2. （2）若种植韭菜的收益等于另两种蔬菜收益之和的2倍，求这时x的值．
3. （3）求王爷爷的蔬菜总收益为W关于x的函数表达式及W的最大值．
答案解析收藏纠错 + 选题
24. (2018·苍南模拟) 如图，矩形ABCD中，AD=10，CD=15，E是边CD上一点，且DE=5，P是射线AD上一动点，过A，P，E三点的⊙O交直线AB于点F，连结PE，EF，PF，设AP=m．
1. （1）当m=6时，求AF的长．
2. （2）在点P的整个运动过程中．
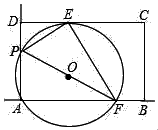
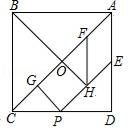
  ①tan∠PFE的值是否改变？若不变，求出它的值；若改变，求出它的变化范围．
  
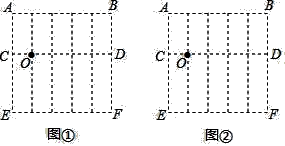
  ②当矩形ABCD恰好有2个顶点落在⊙O上时，求m的值．
3. （3）若点A，H关于点O成中心对称，连结EH，CH．当△CEH是等腰三角形时，求出所有符合条件的m的值．（直接写出答案即可）
答案解析收藏纠错 + 选题