
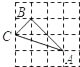
 B .
B .  C .
C .  D .
D . 
①两个相似三角形的面积比等于相似比的平方;
②两个相似三角形对应高的比等于相似比;
③已知△ABC及位似中心O,能够作一个且只能作一个三角形,使位似比为0.5.
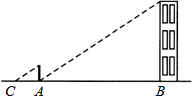
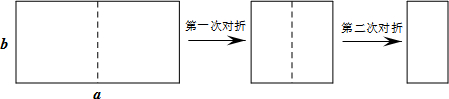
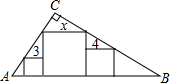
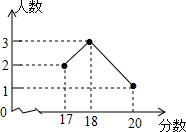
如图所示,n+1个直角边长为1的等腰直角三角形,斜边在同一直线上,设△B2D1C1的面积为S1 , △B3D2C2的面积为S2 , …,△Bn+1DnCn的面积为Sn , 则S1= ,Sn= (用含n的式子表示). 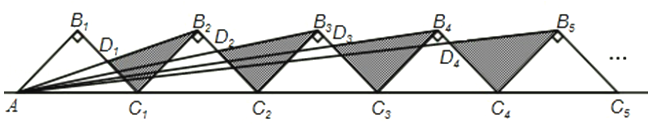
|
|
平均数(分) |
众数(分) |
中位数(分) |
最高成绩(分) |
方差(分2) |
|
小明 |
13 |
10 |
|
17 |
8.25 |
|
小兵 |
13 |
|
13 |
|
1.25 |
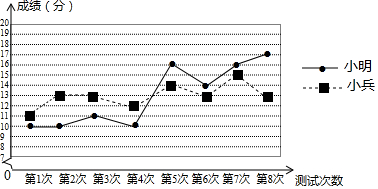
从平均数的角度分析,二人的实力;
从众数的角度分析,的成绩更好;
从最高成绩分析,的成绩更好;
从方差的角度分析,的成绩更稳定;
综合以上四个方面的分析,教练应选择参加比赛.
|
项目 |
第一次锻炼 |
第二次锻炼 |
|
步数(步) |
10000 |
① ▲ |
|
平均步长(米/步) |
0.6 |
② ▲ |
|
距离(米) |
6000 |
7020 |
注:步数×平均步长=距离.
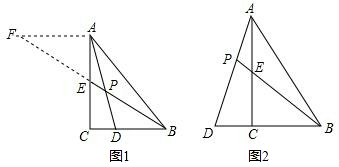
发现:如图1,点D在BC边上,CD:BD=1:2,AD与BE相交于点P,过点A作AF∥BC,交BE的延长线于点F,易得 的值为 ▲ .
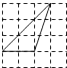
解决问题:如图2,在△ABC中,∠ACB=90°,点D在BC的延长线上,AD与AC边上的中线BE的延长线交于点P,DC:BC=1:2.求 的值:
应用:若CD=2,AC=6,则BP= ▲ .
