2017年山东省日照市经济开发区中考数学一模试卷

更新时间：2024-07-12 浏览次数：881 类型：中考模拟

一、选择题

1. (2017·日照模拟) 下列各数中，最小的数是（）

A . 3^﹣² B . $\text{[math]}$ C . |﹣ $\text{[math]}$ | D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2019·婺城模拟) 以下是我市著名企事业（新飞电器、心连心化肥、新乡银行、格美特科技）的徽标或者商标，其中既是轴对称图形又是中心对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
3. (2017·日照模拟) 2014年巴西世界杯在南美洲国家巴西境内12座城市中的12座球场内举行，本届世界杯的冠军将获得3500万美元的奖励，将3500万用科学记数法表示为（）

A . 3.5×10⁶ B . 3.5×10⁷ C . 35×10⁶ D . 0.35×10⁸

答案解析收藏纠错 + 选题
4. (2020九下·汝南期中) 下列各式计算正确的是（）

A . $\text{[math]}$ =1 B . a⁶÷a²=a³ C . x²+x³=x⁵ D . （﹣x²）³=﹣x⁶

答案解析收藏纠错 + 选题
5. (2017·日照模拟)
用6个完全相同的小正方体组合成如图所示的立体图形，它的俯视图为（　　）

A . B . C . D .

答案解析收藏纠错 + 选题
6. (2022九上·通川月考) 如图是交警在一个路口统计的某个时段来往车辆的车速（单位：千米/时）情况．则这些车的车速的众数、中位数分别是（）

A . 8，6 B . 8，5 C . 52，53 D . 52，52

答案解析收藏纠错 + 选题
7. (2017·日照模拟) 如图，PA、PB是⊙O的切线，AC是⊙O的直径，∠P=62°，则∠BOC的度数为（）

A . 60° B . 62° C . 31° D . 70°

答案解析收藏纠错 + 选题
8. 若不等式组 $\text{[math]}$ 有解，则a的取值范围是（）

A . a＞﹣1 B . a≥﹣1 C . a≤1 D . a＜1

答案解析收藏纠错 + 选题
9. 如图，函数y=kx+b（k≠0）的图象经过点B（2，0），与函数y=2x的图象交于点A，则不等式0＜kx+b＜2x的解集为（）

A . x＞0 B . 0＜x＜1 C . 1＜x＜2 D . x＞2

答案解析收藏纠错 + 选题
10. (2024九下·秀屿月考) 抛物线y=ax²+bx+3（a≠0）过A（4，4），B（2，m）两点，点B到抛物线对称轴的距离记为d，满足0＜d≤1，则实数m的取值范围是（）

A . m≤2或m≥3 B . m≤3或m≥4 C . 2＜m＜3 D . 3＜m＜4

答案解析收藏纠错 + 选题
11. (2017·日照模拟)
如图，已知点P是∠AOB角平分线上的一点，∠AOB=60°，PD⊥OA，M是OP的中点，DM=4cm，如果点C是OB上一个动点，则PC的最小值为（　　）

A . 2 B . 2 $\text{[math]}$ C . 4 D . 4 $\text{[math]}$

答案解析收藏纠错 + 选题
12. (2017·日照模拟) 如图，动点P在平面直角坐标系中按图中箭头所示方向运动，第1次从原点运动到点（1，1），第2次接着运动到点（2，0），第3次接着运动到点（3，2），…，按这样的运动规律，经过第2011次运动后，动点P的坐标是（）

A . （2011，0） B . （2011，1） C . （2011，2） D . （2010，0）

答案解析收藏纠错 + 选题

二、填空题

13. (2017·日照模拟) 计算：（ $\text{[math]}$ +π）⁰﹣2|1﹣sin30°|+（ $\text{[math]}$ ）^﹣¹=．

答案解析收藏纠错 + 选题
14. (2017·日照模拟) 如图，在平面直角坐标系中，矩形OABC的顶点B坐标为（8，4），将矩形OABC绕点O逆时针旋转，使点B落在y轴上的点B′处，得到矩形OA′B′C′，OA′与BC相交于点D，则经过点D的反比例函数解析式是．

答案解析收藏纠错 + 选题
15. (2017·微山模拟) 如图，在△ABC中，∠C=90°，AC=BC，斜边AB=2，O是AB的中点，以O为圆心，线段OC的长为半径画圆心角为90°的扇形OEF，弧EF经过点C，则图中阴影部分的面积为．

答案解析收藏纠错 + 选题
16. (2017·日照模拟) 如图，矩形ABCD中，AB=6，BC=8，点F为BC边上的一个动点，把△ABF沿AF折叠．当点B的对应点B′落在矩形ABCD的对称轴上时，则BF的长为．

答案解析收藏纠错 + 选题

三、解答题

17. (2017·日照模拟) 先化简，再求值：（a+ $\text{[math]}$ ）÷（a﹣2+ $\text{[math]}$ ），其中a满足a²﹣a﹣2=0．

答案解析收藏纠错 + 选题
18. (2017·日照模拟) 在2015年的政府工作报告中提出了九大热词，某数学兴趣小组就A互联网+、B民生底线、C中国制造2.0、D能耗强度等四个热词进行了抽样调查，每个同学只能从中选择一个“我最关注”的热词，如图是根据调查结果绘制的两幅不完整的统计图．
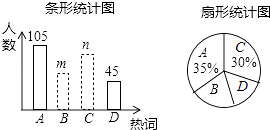
请你根据统计图提供的信息，解答下列问题：
1. （1）本次调查中，一共调查了名同学；
2. （2）条形统计图中，m=，n=；
3. （3）扇形统计图中，热词B所在扇形的圆心角的度数是；
4. （4）从该校学生中随机抽取一个最关注热词D的学生的概率是多少？
答案解析收藏纠错 + 选题
19. (2017·日照模拟) 如图，AB为⊙O的直径，点C为AB延长线上一点，动点P从点A出发沿AC方向以lcm/s的速度运动，同时动点Q从点C出发以相同的速度沿CA方向运动，当两点相遇时停止运动，过点P作AB的垂线，分别交⊙O于点M和点N，已知⊙O的半径为l，设运动时间为t秒．
1. （1）若AC=5，则当t=时，四边形AMQN为菱形；当t=时，NQ与⊙O相切；
2. （2）当AC的长为多少时，存在t的值，使四边形AMQN为正方形？请说明理由，并求出此时t的值．
答案解析收藏纠错 + 选题
20. (2021九上·新泰月考)
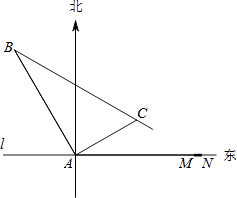
在某飞机场东西方向的地面l上有一长为1km的飞机跑道MN（如图），在跑道MN的正西端14.5千米处有一观察站A．某时刻测得一架匀速直线降落的飞机位于点A的北偏西30°，且与点A相距15千米的B处；经过1分钟，又测得该飞机位于点A的北偏东60°，且与点A相距5 $\text{[math]}$ 千米的C处．
1. （1）该飞机航行的速度是多少千米/小时？（结果保留根号）
2. （2）如果该飞机不改变航向继续航行，那么飞机能否降落在跑道MN之间？请说明理由．
答案解析收藏纠错 + 选题
21. (2017·日照模拟)
问题：如图（1），点E、F分别在正方形ABCD的边BC、CD上，∠EAF=45°，试判断BE、EF、FD之间的数量关系．
1. （1）【发现证明】
  
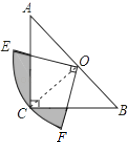
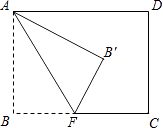
  小聪把△ABE绕点A逆时针旋转90°至△ADG，从而发现EF=BE+FD，请你利用图（1）证明上述结论．
2. （2）【类比引申】
  
  如图（2），四边形ABCD中，∠BAD≠90°，AB=AD，∠B+∠D=180°，点E、F分别在边BC、CD上，则当∠EAF与∠BAD满足关系时，仍有EF=BE+FD．
3. （3）【探究应用】
  
  如图（3），在某公园的同一水平面上，四条通道围成四边形ABCD．已知AB=AD=80米，∠B=60°，∠ADC=120°，∠BAD=150°，道路BC、CD上分别有景点E、F，且AE⊥AD，DF=40（ $\text{[math]}$ ﹣1）米，现要在E、F之间修一条笔直道路，求这条道路EF的长（结果取整数，参考数据： $\text{[math]}$ =1.41， $\text{[math]}$ =1.73）
答案解析收藏纠错 + 选题
22. (2019九上·东台期中)
如图，在直角坐标系中，抛物线经过点A（0，4），B（1，0），C（5，0），其对称轴与x轴相交于点M．
1. （1）求抛物线的解析式和对称轴；
2. （2）在抛物线的对称轴上是否存在一点P，使△PAB的周长最小？若存在，请求出点P的坐标；若不存在，请说明理由；
3. （3）连接AC，在直线AC的下方的抛物线上，是否存在一点N，使△NAC的面积最大？若存在，请求出点N的坐标；若不存在，请说明理由．
答案解析收藏纠错 + 选题