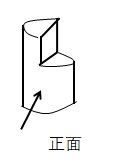
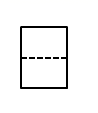
 B .
B .  C .
C . 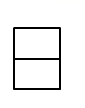 D .
D . 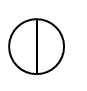
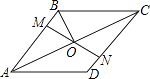
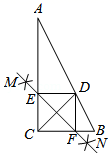
步骤1:分别以点C和点D为圆心,大于 的长为半径作弧,两弧相交于M,N两点;
步骤2:作直线MN,分别交AC,BC于点E,F;
步骤3:连接DE,DF;
若AC=4,BC=2,则线段DE的长为
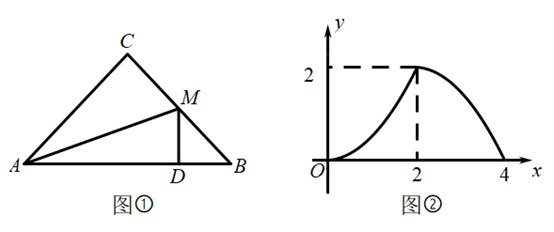
|
初一 |
96 |
100 |
89 |
95 |
62 |
75 |
93 |
86 |
86 |
93 |
|
95 |
95 |
88 |
94 |
95 |
68 |
92 |
80 |
78 |
90 |
|
|
初二 |
100 |
98 |
96 |
95 |
94 |
92 |
92 |
92 |
92 |
92 |
|
86 |
84 |
83 |
82 |
78 |
78 |
74 |
64 |
60 |
92 |
通过整理,两组数据的平均数、中位数、众数和方差如表:
|
年级 |
平均数 |
中位数 |
众数 |
方差 |
|
初一 |
87.5 |
91 |
m |
96.15 |
|
初二 |
86.2 |
n |
92 |
113.06 |
某同学将初一学生得分按分数段( ,
,
,
),绘制成频数分布直方图,初二同学得分绘制成扇形统计图,如图(均不完整),初一学生得分频数分布直方图 初二学生得分扇形统计图(注:x表示学生分数)
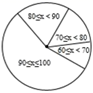
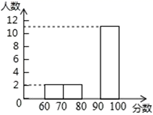
请完成下列问题:
①当 的长为时,四边形
为菱形;
②若 .则
的长为.
活动一
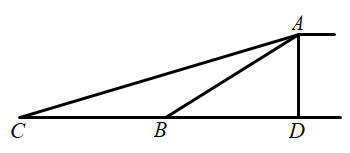
如图3,将铅笔 绕端点A顺时针旋转,
与
交于点D,当旋转至水平位置时,铅笔
的中点C与点O重合.
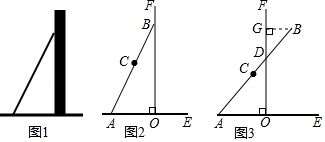
设 ,点B到
的距离
.
①用含x的代数式表示: 的长是
,
的长是
;
②y与x的函数关系式是,自变量x的取值范围是.
①列表:根据(1)中所求函数关系式计算并补全表格.
|
| 6 | 5 | 4 | 3.5 | 3 | 2.5 | 2 | 1 | 0.5 | 0 |
| | 0 | 0.55 | 1.2 | 1.58 | 1.0 | 2.47 | 3 | 4.29 | 5.08 |
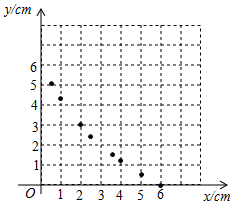
②描点:根据表中数值,描出①中剩余的两个点 .
③连线:在平面直角坐标系中,请用平滑的曲线画出该函数的图象.
请你结合函数的图象,写出该函数的两条性质或结论.
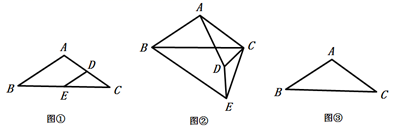
如图①,在 中,
,
,
,点
分别是
的中点,连接,则
的值为.
若将 绕点C逆时针方向旋转一周,在旋转过程中
的值有没有变化?以图②的情形给出证明.
如图③,当 旋转到
三点在同一条直线上是,直接写出
的长.
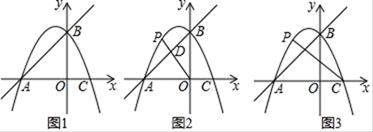
①如图2,若点P在直线AB上方,连接OP交AB于点D , 求 的最大值;
②如图3,若点P在x轴的上方,连接PC , 以PC为边作正方形CPEF , 随着点P的运动,正方形的大小、位置也随之改变.当顶点E或F恰好落在y轴上,直接写出对应的点P的坐标.