

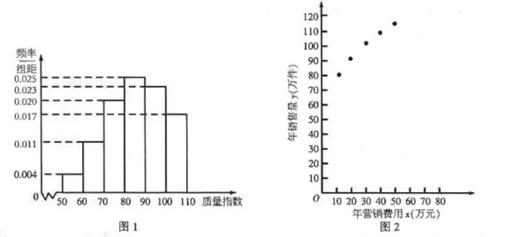
产品的质量指数在 的为三等品,在
的为二等品,在
的为一等品,该产品的三、二、一等品的销售利润分别为每件1.5,3.5,5.5(单位:元),以这100件产品的质量指数位于各区间的频率代替产品的质量指数位于该区间的概率.
| | | | |
| 16.30 | 24.87 | 0.41 | 1.64 |
表中 ,
,
,
根据散点图判断, 可以作为年销售量
(万件)关于年营销费用
(万元)的回归方程.
(ⅰ)建立 关于
的回归方程;
(ⅱ)用所求的回归方程估计该公司应投入多少营销费,才能使得该产品一年的收益达到最大?(收益=销售利润-营销费用,取 )
参考公式:对于一组数据: ,
,
,
,其回归直线
的斜率和截距的最小乘估计分别为
,