 B .
B .  C .
C . 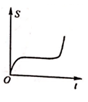 D .
D . 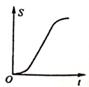
,其中a=1+
,b=-1+
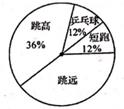
复选人员统计表:
|
项目/人数/性别 |
男 |
女 |
|
短跑 |
1 |
2 |
|
跳远 |
a |
6 |
|
乒乓球 |
2 |
1 |
|
跳高 |
3 |
b |
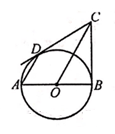
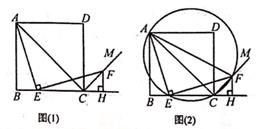
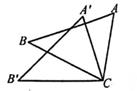
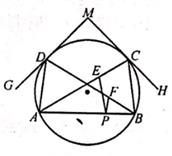
小聪说,∠CDA+∠AOC的值是一个固定的值;
小明说,∠CDA+∠AOC的值随∠A度数的变化而变化。
若∠CDA+∠AOC的值为y,∠A度数为x.你认为他们之中谁说的是正确的?若你认为小聪说的正确,请你求出这个固定值:若你认为小明说的正确,请你求出y与x之间的关系.