2017年浙江省永康市初中毕业生适应性考试数学卷

更新时间：2017-05-16 浏览次数：849 类型：中考模拟

一、一、选择题

1. (2017·永康模拟) －2017的相反数是（）

A . $\text{[math]}$ B . 2017 C . －2017 D . － $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2017·永康模拟)
如图，已知a∥b，∠1=68°，则∠2=（）

A . 22° B . 68° C . 102° D . 112°

答案解析收藏纠错 + 选题
3. (2023九上·瑞安月考) 抛物线 $\text{[math]}$ 先向右平移1个单位，再向下平移3个单位得到的抛物线解析式为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2024七下·张店期中) 下列运算正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2020·温州模拟)
如图物体的主视图是（）

A . B . C . D .

答案解析收藏纠错 + 选题
6. (2017·永康模拟) 分式方程 $\text{[math]}$ 的解是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2017·永康模拟)
如图，在△ABC中，点D，E分别在AB，AC上，且 $\text{[math]}$ ，则 $\text{[math]}$ ： $\text{[math]}$ （）

A . 1：2 B . 1：4 C . 1：8 D . 1：9

答案解析收藏纠错 + 选题
8. (2019·北仑模拟) 某校7个班同学积极捐出自己的零花钱献爱心，各班捐款的数额分别是（单位：元）：500，200，500，300，500，250，1350．这组数据的众数和中位数分别是（）

A . 500，200 B . 500，500 C . 500，300 D . 1350，500

答案解析收藏纠错 + 选题
9. (2019·兰坪模拟) 不等式组 $\text{[math]}$ 的解在数轴上表示为（ )

A . B . C . D .

答案解析收藏纠错 + 选题
10. (2017·永康模拟) 已知A，B两地相距80km，甲，乙两人沿同一条公路从A地出发到B地，乙骑自行车，甲骑摩托车．图中DE，OC分别表示甲，乙离开A地的路程s（km）与时间t（h）的函数关系，根据图象得出的下列信息错误的是（）

A . 乙到达B地时甲距A地120km B . 乙出发1.8小时被甲追上 C . 甲，乙相距20km时，t为2.4h D . 甲的速度是乙的速度的 $\text{[math]}$ 倍

答案解析收藏纠错 + 选题

二、填空题

11. (2024九下·蓬江模拟) 因式分解： $\text{[math]}$ =.

答案解析收藏纠错 + 选题
12. (2017·永康模拟) 函数 $\text{[math]}$ 自变量x的取值范围是．

答案解析收藏纠错 + 选题
13. (2017·永康模拟)
如图，⊙O是△ABC的外接圆，∠AOB=70°，AB＝AC，则∠ABC=．

答案解析收藏纠错 + 选题
14. (2019·北仑模拟) 一个布袋里放有红色、黄色、黑色三种球，它们除颜色外其余都相同.红色、黄色、黑色的个数之比为4:3:2,则从布袋里任意摸出1个球不是红球的概率是．

答案解析收藏纠错 + 选题
15. (2017·永康模拟)
如图，正方形ABCD的边长为13，以CD为斜边向外作Rt△CDE，若点A到CE的距离为17，则CE=．

答案解析收藏纠错 + 选题
16. (2017·永康模拟)
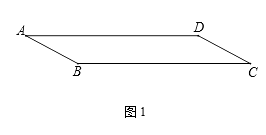
一张宽为6cm的平行四边形纸带ABCD如图1所示，AB=10cm，小
明用这张纸带将底面周长为10cm直三棱柱纸盒的侧面进行包贴（要求包
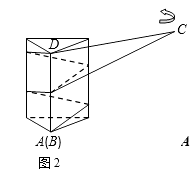
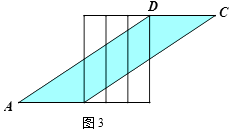
贴时没有重叠部分）. 小明通过操作后发现此类包贴问题可将直三棱柱的
侧面展开进行分析．
1. （1）若纸带在侧面缠绕三圈，正好将这个直三棱柱纸盒的侧面全部包贴满．则纸带AD的长度为 cm；
2. （2）若AD=100cm，纸带在侧面缠绕多圈，正好将这个直三棱柱纸盒的侧面全部包贴满.则这个直三棱柱纸盒的高度是cm．
答案解析收藏纠错 + 选题

三、解答题

17. (2017·永康模拟) 计算： $\text{[math]}$

答案解析收藏纠错 + 选题
18. (2017·永康模拟) 先化简，再求值：
$\text{[math]}$ ,其中x=2.

答案解析收藏纠错 + 选题
19. (2017·永康模拟)
如图所示，在▱ABCD中，对角线AC与BD相交于点O，过点O作一条直线分别交AB，CD于点E，F．
1. （1）求证：OE＝OF；
2. （2）若AB＝6，BC＝5，OE＝2，求四边形BCFE的周长．
答案解析收藏纠错 + 选题
20. (2017·永康模拟)
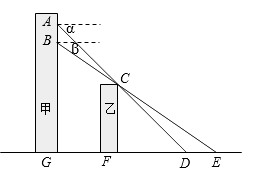
小张在甲楼A处向外看，由于受到前面乙楼的遮挡，最近只能看到地面D处，俯角为α．小颖在甲楼B处（B在A的正下方）向外看，最近能看到地面E处，俯角为β，地面上G，F，D，E在同一直线上，已知乙楼高CF为10m，甲乙两楼相距FG为15m，俯角α=45°，β=35°．
1. （1）求点A到地面的距离AG；
2. （2）求A，B之间的距离．(结果精确到0.1m)（sin35°≈0.57，cos35°≈0.82，tan35°≈0.70）
答案解析收藏纠错 + 选题
21. (2017·永康模拟)
学校计划在七年级学生中开设4个信息技术应用兴趣班，分别为“无人机”班，“3D打印”班，“网页设计”班，“电脑绘画”班，规定每人最多参加一个班，自愿报名．根据报名情况绘制了下面统计图表，请回答下列问题：
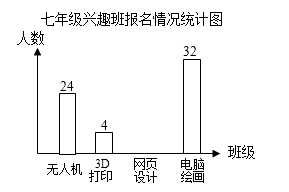
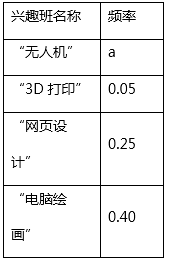
七年级兴趣班报名情况统计表
1. （1）报名参加兴趣班的总人数为人；统计表中的a=；
2. （2）将统计图补充完整；
3. （3）为了均衡班级人数，在“电脑绘画”班中至少动员几人到“3D打印”班，才能使“电脑绘画”班人数不超过“3D打印”班人数的2倍？
答案解析收藏纠错 + 选题
22. (2017·永康模拟)
如图，OA，OB是⊙O的两条半径，OA⊥OB，C是半径OB上一动点，连结AC并延长交⊙O于D，过点D作圆的切线交OB的延长线于E，已知OA＝8．
1. （1）求证：∠ECD＝∠EDC；
2. （2）若tanA＝ $\text{[math]}$ ，求DE长；
3. （3）当∠A从15°增大到30°的过程中，求弦AD在圆内扫过的面积．
答案解析收藏纠错 + 选题
23. (2017·永康模拟) 综合题
1. （1）
  探究：如图1 ，直线l与坐标轴的正半轴分别交于A，B两点，与反比例函数 $\text{[math]}$ $\text{[math]}$ 的图象交于C，D两点(点C在点D的左边)，过点C作CE⊥y轴于点E，过点D作DF⊥x轴于点F，CE与DF交于点G(a ， b).
  ①若 $\text{[math]}$ ，请用含n的代数式表示 $\text{[math]}$ ；
  ②求证： $\text{[math]}$ ；
2. （2）
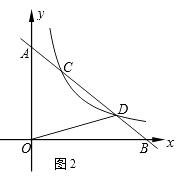
  应用：如图2，直线l与坐标轴的正半轴分别交于点A，B两点，与反比例函数 $\text{[math]}$ $\text{[math]}$ 的图象交于点C，D两点(点C在点D的左边)，已知 $\text{[math]}$ ，△OBD的面积为1，试用含m的代数式表示k.
答案解析收藏纠错 + 选题
24. (2017·永康模拟)
已知，抛物线y=ax²+bx+4与x轴交于点A（-3，0）和B（2，0），与y轴交于点C．
1. （1）求抛物线的解析式；
2. （2）如图1，若点D为CB的中点，将线段DB绕点D旋转，点B的对应点为点G，当点G恰好落在抛物线的对称轴上时，求点G的坐标；
3. （3）如图2，若点D为直线BC或直线AC上的一点，E为x轴上一动点，抛物线
  $\text{[math]}$ 对称轴上是否存在点F，使以B，D，F，E为顶点的四边形为菱形？若存在，请求出点F的坐标；若不存在，请说明理由．
答案解析收藏纠错 + 选题