浙江省温州市六校2020年数学中考模拟联考试

更新时间：2020-06-11 浏览次数：435 类型：中考模拟

一、选择题(本题有10小题，每小题4分，共40分.)

1. (2020·温州模拟) 在|-2|，-(+2)，2^-1 ， 0这四个数中，最小的数是（）

A . |-2| B . -(+2) C . 0 D . 2^-1

答案解析收藏纠错 + 选题
2. (2020·温州模拟) 近期，新型冠状病毒感染肺炎的疫情在全国蔓延，全国人民团结一致，全力抗击新型冠状病毒感染肺炎.社会各界人士积极捐款。截止2月5日中午12点，武汉市慈善总会接收捐赠款约3230000000元。将3230000000用科学记数法表示应为（）

A . 323×10⁷ B . 32.3×10⁸ C . 3.23×10⁹ D . 3.23×10¹⁰

答案解析收藏纠错 + 选题
3. (2020·温州模拟)
如图物体的主视图是（）

A . B . C . D .

答案解析收藏纠错 + 选题
4. (2020·苏州模拟) 如图，一个圆形飞镖板被分为四个圆心角相等的扇形，若大圆半径为2，小圆半径为1，则阴影部分的面积为（）

A . π B . $\text{[math]}$ π C . 3π D . $\text{[math]}$ π

答案解析收藏纠错 + 选题
5. (2020·莫旗模拟) 如图，小猫在5×5的地板砖上行走，并随机停留在某一块方砖上，则它停留在阴影方砖上的概率是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2020·温州模拟) 下列抛物线中，其顶点在反比例函数y= $\text{[math]}$ 的图象上的是（）

A . y=(x-4)²+3 B . y=(x-4)²-3 C . y=(x+2)²+1 D . y=(x+2)²-1

答案解析收藏纠错 + 选题
7. (2023八下·颍州期末) 如图，小明将一张长为20cm，宽为15cm的长方形纸(AE>DE)剪去了一角，量得AB=3cm，CD=4cm，则剪去的直角三角形的斜边长为（）

A . 5cm B . 12cm C . 16cm D . 20cm

答案解析收藏纠错 + 选题
8. (2020·温州模拟) 如图，在平面直角坐标系中，在x轴、y轴的半轴上分别截取OA，OB，使OA=OB，再分别以点A，B为圆心，以大于 $\text{[math]}$ AB长为半径作弧，两弧交于点C.若点C的坐标为(m-1，2n)，则m与n的关系为（）

A . m+2n=1 B . m-2n=1 C . 2n-m=1 D . n-2m=1

答案解析收藏纠错 + 选题
9. (2020·温州模拟) 已知二次函数y=x²-2x+2(其中x是自变量)，当0≤x≤a时，y的最大值为2，y的最小值为1，则a的值为（）

A . a=1 B . 1≤a<2 C . 1<a≤2 D . 1≤a≤2

答案解析收藏纠错 + 选题
10. (2020·温州模拟) 点C是半径为1的半圆弧AB的一个三等分点，分别以弦AC、BC为直径向外侧作2个半圆，点D、E也分别是2半圆弧的三等分点，再分别以弦AD、DC、CE、BE为直径向外侧作4个半圆。则图中阴影部分(4个新月牙形)的面积和是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题(本题有6小题，每小题5分，共30分)

11. (2021八上·盐池期末) 若a²+2a=4，则(a+1)²=。

答案解析收藏纠错 + 选题
12. (2020·温州模拟) 不等式组 $\text{[math]}$ 的解集为。

答案解析收藏纠错 + 选题
13. (2020·温州模拟) 一组数据：23，27，20，18，x，16.它们的平均数是21，则中位数为。

答案解析收藏纠错 + 选题
14. (2020·温州模拟) 如图，在⊙O中过O作OC⊥AB于C，连接AO并延长，交过B点的⊙O的切线于D点，若AB=8，BD=12，OC=3，则AD= 。

答案解析收藏纠错 + 选题
15. (2020·温州模拟) 如图，矩形ABCD中，AB=10，BC=6，P为AD上一点，将△ABP沿BP翻折至△EBP，PE与CD相交于点O，当OE=OD时，AP的长为。

答案解析收藏纠错 + 选题
16. (2020·温州模拟) 图1是一张可以折叠的小床展开后支撑起来放在地面的示意图，此时点A、B、C在同一直线上，且∠ACD=90°，图2是小床支撑脚CD折叠的示意图，在折叠过程中，△ACD变形为四边形ABC'D'，最后折叠形成一条线段BD”。某家装厂设计的折叠床是AB=8cm，BC=16cm，①此时CD应该是多长。②折叠时，当AB⊥BC'时，sinD'=。

答案解析收藏纠错 + 选题

三、解答题(本题有8小题，共80分。)

17. (2020·温州模拟)
1. （1）计算：(π-3.14)⁰-2 $\text{[math]}$ cos30°+( $\text{[math]}$ )^-2
2. （2）化简： $\text{[math]}$
答案解析收藏纠错 + 选题
18. (2020八上·青龙期末) 如图，在△ABC中，边AB、AC的垂直平分线分别交BC于D、E.
1. （1）若BC=5，求△ADE的周长.
2. （2）若∠BAD+∠CAE=60°，求∠BAC的度数.
答案解析收藏纠错 + 选题
19. (2020·温州模拟) 新冠疫情期间，某学校为了更好地帮助学生进行网上学习，随机调查了本校部分初三学生的学习成果。并将其分为A，B，C，D四种类型(分别对应优、良、合格、待合格)。现根据调查的数据绘制成如下的条形统计图和扇形统计图。
请根据以上不完整的统计图提供的信息，解答下列问题：
1. （1）该校共调查了名同学的学习成果？
2. （2）补全条形统计图和扇形统计图；
3. （3）若该校初三一共有500名学生。开学后学校计划把C和D等级的同学平均分成了四个班级，利用课后时间来巩固网课内容。已知小红和小玲都在C，D两组里面，问他们分到一个班进行巩固学习的概率有多大。(利用树状图或表格解答)
答案解析收藏纠错 + 选题
20. (2020·温州模拟) 6×6的方格图中，按要求作格点三角形ABC。
1. （1）在图1中，作等腰直角△ABC，使得∠BAC=45°；(画出一个即可)
2. （2）在图2中，作平行四边形ABCD，使得∠BAD=45°。
答案解析收藏纠错 + 选题
21. (2020·温州模拟) 已知：如图，以BC为直径作⊙O，AC切⊙O于点C，连接AB，交⊙O于点D，E为 $\text{[math]}$ 上一点，CE、DB交于点F且AC=AF。
1. （1）求证：E为 $\text{[math]}$ 的中点。
2. （2）若CF=8，EF=2，求⊙O的半径。
答案解析收藏纠错 + 选题
22. (2020·温州模拟) 如图，已知二次函数y=ax²-2ax+c(a<0)的图象交x轴于A、B两点，交y轴于点C。过点A的直线y=kx+2k(k≠0)与这个二次函数的图象的另一个交点为F，与该图象的对称轴交于点E，与y轴交于点D，且DE=EF。
1. （1）求点A，点B的坐标，并把c用a表示；
2. （2）若△BDF的面积为12，求这个二次函数的关系式。
答案解析收藏纠错 + 选题

23. (2020·温州模拟) 温州某一企业原先一次性口罩和防雾霾口罩生产信息如下表：

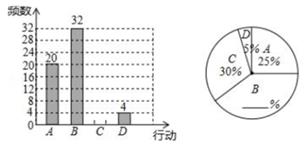
口罩类型	材料成本(不含人工)	出厂价	产量(一人一天)
一次性口罩	0.1元/个	0.2元/个	2000个
防雾霾口罩	2.5元/个	4元/个	200个

已知该企业有12名工人，工资每人每天150元。该企业原来每天产量共15000个口罩。

（1）求原先企业安排生产一次性口罩和防雾霾口罩各有多少人。
（2）经一段时间运行，企业发现每天销售的防雾霾口罩，最多只能卖900个。而一次性口罩可以全部销售，市场缺口较大。怎么安排生产口罩的人数可以使该企业每一天获得利润最大。最大利润是多少？(注：没有销售的口罩，作为库存暂时当做不赚不亏)。

（3）在疫情期间，为了配合政府防疫工作，该厂改为全部生产一次性口罩。因为原材料价格暴涨，口罩的材料成本和出厂价分别变为0.6元/个和1元/个。一部分员工因为滞留在外，无法及时回来工作。所以该厂提高了剩余老员工的工资，也招募了几个新员工过来且老员工人数多于新员工。信息如下表：

员工类型	每日工资	一次性口罩产量(一人一天)
老员工	300元/天	2000个
新员工	200元/天	1000个

要是该厂的利润达到4000元/天。求该厂留下来的老员工和招募的新员工人数。

答案解析收藏纠错 + 选题

24. (2020·温州模拟) 在矩形ABCD中，点E是AD上一动点，连结BE，过点E作EF⊥BE，交CD于F，以EF为直径作⊙O。设AE=t。
1. （1）求证∠1=∠2；
2. （2）如图2，已知AD=8，连结BF，交⊙O于点G，并连结EG，DG，
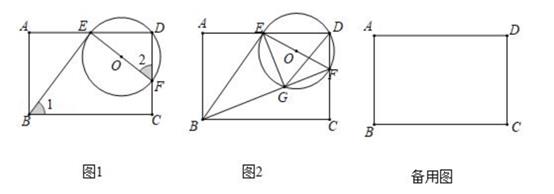
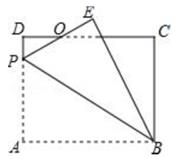
  ①当AB=6时，若△EGD是以EG为腰的等腰三角形，求t的值；
  
  ②连接OC，GC，当tan∠FBC= $\text{[math]}$ ，OC∥EG时，求t的值。
3. （3） OC交BF于点P，当tan∠1=1，OC∥EG时，记△OFP的面积为S₁ ， △CGP的面积为S₂ ，四边形EGCF的面积为S₃ ，请直接写出 $\text{[math]}$ 的值。
答案解析收藏纠错 + 选题

试卷信息

小学

初中

高中

浙江省温州市六校2020年数学中考模拟联考试

副标题：

*注意事项：

浙江省温州市六校2020年数学中考模拟联考试

试题分析

总体分析

题量分析

难度分析

知识点分析