 B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 



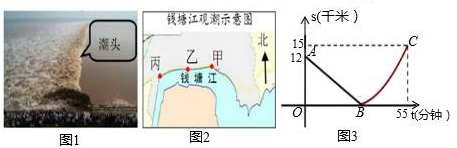
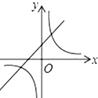
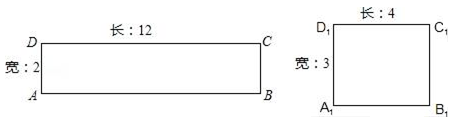
按上述信息,小红将“交叉潮”形成后潮头与乙地之间的距离s(千米)与时间t(分钟)的函数关系用图3表示,其中:“11:40时甲地‘交叉潮’的潮头离乙地12千米”记为点A(0,12),点B坐标为(m,0),曲线BC可用二次函数s= t2+bt+c(b,c是常数)刻画.
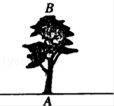


请你解决下列问题:
