 B .
B . 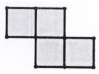 C .
C . 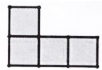 D .
D . 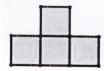


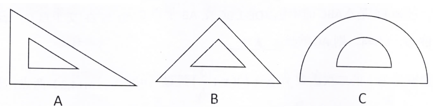
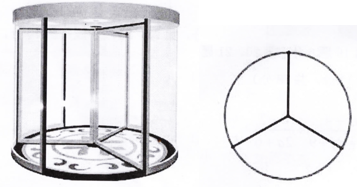
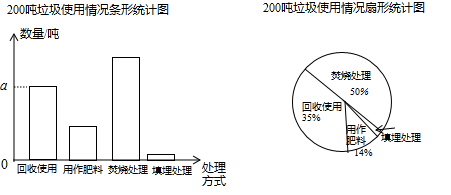
①直接写出紧急情况时旋转门每分钟可以出去人;
②该写字楼有9层,每层10间办公室,平均每个办公室6人。为了符合消防安全要求,要在一楼再安装几道普通侧门,每道侧门每分钟能通过45人。在紧急情况下,要使整幢写字楼的人能在5分钟内全部安全撤离(下楼时间忽略不计),至少要安装几道普通侧门.

|
单位底位置 |
... |
-3~-2 |
-2~-l |
-l~0 |
0~1 |
1~2 |
2~3 |
3~4 |
... |
|
矩形条高 |
… |
1 |
... |
... |
3.5 |
... |
... |
15 |
... |
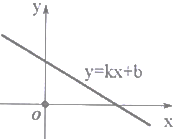
看所有矩形条的左上顶点都在同一个我们已学的某类函数图象上。


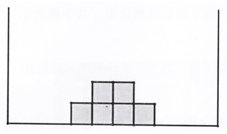
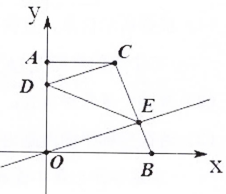
①在图2、图3的正方形网格中,请你仅用直尺作出矩形ABCD的台球四边形(其中格点E为台球四边形的一个顶点)
②借助图形,小明进一步探究台球四边形的性质,得到了如下两个猜想,请你判断(对的打√,错的打×).
a.一个矩形的台球四边形的周长等于这个矩形两条对角线的和()
b.一个矩形的台球四边形的面积不超过这个矩形面积的一半()
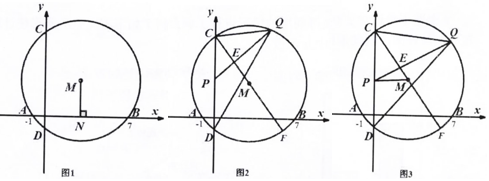
①判断线段PQ与直径CF的位置关系,并说明理由;
②求CQ的长;