2016-2017学年江苏省盐城市盐都区九年级下学期期中数学...

更新时间：2017-05-26 浏览次数：1292 类型：期中考试

一、选择题

1. (2017九下·盐都期中) $\text{[math]}$ 的倒数是（）

A . ﹣3 B . $\text{[math]}$ C . 3 D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2017九下·盐都期中) 下列计算正确的是（　　）

A . 2a﹣a=1 B . a²+a²=2a⁴ C . a²•a³=a⁵ D . （a﹣b）²=a²﹣b²

答案解析收藏纠错 + 选题
3. (2017九下·盐都期中) 不等式组 $\text{[math]}$ 的解集是（）

A . x＞1 B . 1＜x≤2 C . x≤2 D . 无解

答案解析收藏纠错 + 选题
4. (2017九下·盐都期中) 一个几何体的三视图如图所示，则这个几何体是（）

A . B . C . D .

答案解析收藏纠错 + 选题
5. (2017九下·盐都期中) 对于一组统计数据：3，3，6，3，5，下列说法中错误的是（）

A . 中位数是6 B . 众数是3 C . 平均数是4 D . 方差是1.6

答案解析收藏纠错 + 选题
6. (2017九下·盐都期中)
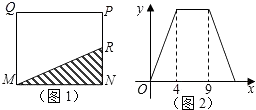
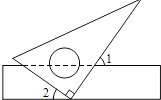
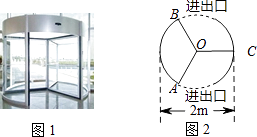
如图1，在矩形MNPQ中，动点R从点N出发，沿着N→P→Q→M方向运动至点M处停下，设点R运动的路程为x，△MNR的面积为y，如果y关于x的函数图象如图2所示，则下列说法不正确的是（）

A . 当x=2时，y=5 B . 矩形MNPQ的面积是20 C . 当x=6时，y=10 D . 当y= $\text{[math]}$ 时，x=3

答案解析收藏纠错 + 选题

二、填空题

7. (2022八下·包河期末) 若二次根式 $\text{[math]}$ 有意义，则x的取值范围是．

答案解析收藏纠错 + 选题
8. (2017九下·盐都期中) “十二五”期间，将新建保障性住房约37000000套，用于解决中低收入和新参加工作的大学生住房的需求，把37000000用科学记数法表示应该是．

答案解析收藏纠错 + 选题
9. (2017九下·盐都期中) 如图，将三角板的直角顶点放在直尺的一边上，若∠1=55°，则∠2的度数为°．

答案解析收藏纠错 + 选题
10. (2017九下·盐都期中) 小燕抛一枚硬币10次，有7次正面朝上，当她抛第11次时，正面向上的概率为．

答案解析收藏纠错 + 选题
11. (2017九下·盐都期中) 如图，⊙O的内接四边形ABCD中，∠BOD=100°，则∠BCD=．

答案解析收藏纠错 + 选题
12. (2017九下·盐都期中) 若a﹣2b=2，则6﹣3a+6b的值为．

答案解析收藏纠错 + 选题
13. (2017九下·盐都期中) 三翼式旋转门在圆柱形的空间内旋转，旋转内的三片旋转翼把空间等分成三个部分，如图1，旋转门的俯视图是直径的2米的圆，图2显示了某一时刻旋转翼的位置，则弧AB的长是米．（结果保留π）

答案解析收藏纠错 + 选题
14. (2017九下·盐都期中) 如图，在△ABC中，∠C=90°，AC=6，BC=8，点D、M分别在BC、AC上，Rt△BDE、Rt△EFG、Rt△GHI、Rt△IJK、Rt△KMA的斜边都在AB上，则五个小直角三角形的周长和为．

答案解析收藏纠错 + 选题
15. (2017九下·盐都期中) 定义：如果三角形有一边上的中线恰好等于这边的长，那么称这个三角形为“匀称三角形”．若Rt△ABC为匀称三角形，且∠C=90°，AC=4，则BC=．

答案解析收藏纠错 + 选题
16. (2017九下·盐都期中)
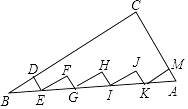
如图，已知A₁ ， A₂ ， A₃ ， …A_n是x轴上的点，且OA₁=A₁A₂=A₂A₃=…=A_n_﹣₁A_n=1，分别过点A₁ ， A₂ ， A₃ ， …A_n作x轴的垂线交反比例函数y= $\text{[math]}$ （x＞0）的图象于点B₁ ， B₂ ， B₃ ， …B_n ，过点B₂作B₂P₁⊥A₁B₁于点P₁ ，过点B₃作B₃P₂⊥A₂B₂于点P₂…，记△B₁P₁B₂的面积为S₁ ， △B₂P₂B₃的面积为S₂…，△B_nP_nB_n₊₁的面积为S_n ，则S₁+S₂+S₃+…+S_n=．

答案解析收藏纠错 + 选题

三、解答题

17. (2017九下·盐都期中) 计算：|﹣8|+（﹣2）³+tan45°﹣ $\text{[math]}$ ．

答案解析收藏纠错 + 选题
18. (2018·余姚模拟) 先化简，再求值：（1+ $\text{[math]}$ ）÷ $\text{[math]}$ ，其中x= $\text{[math]}$ ﹣1．

答案解析收藏纠错 + 选题
19. (2017九下·盐都期中) 如图，转盘被等分成6个扇形，每个扇形上依次标有数字1，2，3，4，5，6．在游戏中特别规定：当指针指向边界时，重新转动转盘．
1. （1）自由转动转盘，当它停止转动时，指针指向的数大于4的概率为；
2. （2）请用画树状图法或列表法等方式求出“两次转动转盘，指针指向的数都大于4”的概率．
答案解析收藏纠错 + 选题
20. (2017九下·盐都期中) 某学校九年级学生举行朗诵比赛，全年级学生都参加，学校对表现优异的学生进行表彰，设置一、二、三等奖各进步奖共四个奖项，赛后将九年级（1）班的获奖情况绘制成如图所示的两幅不完整的统计图，请根据图中的信息，解答下列问题：
1. （1）九年级（1）班共有名学生；
2. （2）将条形图补充完整：在扇形统计图中，“二等奖”对应的扇形的圆心角度数是；
3. （3）如果该九年级共有1250名学生，请估计荣获一、二、三等奖的学生共有多少名．
答案解析收藏纠错 + 选题
21. (2017九下·盐都期中) 如图，在▱ABCD中，对角线AC，BD交于点O，E为AB中点，点F在CB的延长线上，且EF∥BD．
1. （1）求证；四边形OBFE是平行四边形；
2. （2）当线段AD和BD之间满足什么条件时，四边形OBFE是矩形？并说明理由．
答案解析收藏纠错 + 选题
22. (2017九下·盐都期中) 如图，AB是⊙O的直径，D为⊙O上一点，过 $\text{[math]}$ 上一点T作⊙O的切线TC，且TC⊥AD于点C．
1. （1）若∠DAB=50°，求∠ATC的度数；
2. （2）若⊙O半径为2，CT= $\text{[math]}$ ，求AD的长．
答案解析收藏纠错 + 选题
23. (2022·广东模拟) 如图，矩形OABC的顶点A、C分别在x、y轴的正半轴上，点D为BC边上的点，反比例函数y= $\text{[math]}$ （k≠0）在第一象限内的图象经过点D（m，2）和AB边上的点E（3， $\text{[math]}$ ）．
1. （1）求反比例函数的表达式和m的值；
2. （2）将矩形OABC的进行折叠，使点O于点D重合，折痕分别与x轴、y轴正半轴交于点F，G，求折痕FG所在直线的函数关系式．
答案解析收藏纠错 + 选题
24. (2017九下·盐都期中) 如图1是一种折叠椅，忽略其支架等的宽度，得到他的侧面简化结构图（图2），支架与坐板均用线段表示，若座板DF平行于地面MN，前支撑架AB与后支撑架AC分别与座板DF交于点E、D，现测得DE=20厘米，DC=40厘米，∠AED=58°，∠ADE=76°．
1. （1）求椅子的高度（即椅子的座板DF与地面MN之间的距离）（精确到1厘米）
2. （2）求椅子两脚B、C之间的距离（精确到1厘米）（参考数据：sin58°≈0.85，cos58°≈0.53，tan58°≈1.60，sin76°≈0.97．cos76°≈0.24，tan76°≈4.00）
答案解析收藏纠错 + 选题
25. (2017九下·盐都期中) 某公司开发出一种高科技电子节能产品，投资2500万元一次性购买整套生产设备，此外生产每件产品需成本20元，每年还需投入500万广告费，按规定该产品的售价不得低于30元/件且不得高于70元/件，该产品的年销售量y（万件）与售价x（元/件）之间的函数关系如下表：
x（元/件）
30
31
…
70
y（万件）
120
119
…
80
1. （1）求y与x的函数关系式，并写出x的取值范围；
2. （2）第一年公司是盈利还是亏损？冰球出当盈利最大或亏损最小时该产品的售价；
3. （3）在（2）的前提下，即在第一年盈利最大或亏损最小时，第二年公司重新确定产品定价，能否使两年盈利3500万元？若能，求第二年产品的售价；若不能，说明理由．
答案解析收藏纠错 + 选题
26. (2017九下·盐都期中) 探究题
1. （1）
  问题发现
  如图1，△ABC和△BDE均为等边三角形，点A，D，E在同一直线上，连接CD．填空；
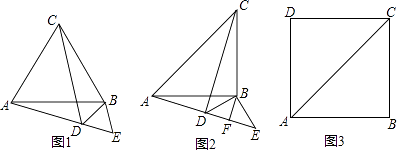
  ①CDB的度数为；
  ②线段AE，CD之间的数量关系为．
2. （2）拓展探究
  如图2，△ABC和△DBE均为等腰直角三角形，∠ABC=∠DBE=90°，点A，D，E在同一直线上，BF为△DBE中DE边上的高，连接CD．
  ①求∠CDB的大小；
  ②请判断线段BF，AD，CD之间的数量关系，并说明理由．
3. （3）解决问题
  如图3，在正方形ABCD中，AC=2 $\text{[math]}$ ，AE=1，CE⊥AE于E，请补全图形，求点B到CE的距离．
答案解析收藏纠错 + 选题
27. (2017九下·盐都期中)
如图1，二次函数y= $\text{[math]}$ x²+bx+c与一次函数y= $\text{[math]}$ x﹣3的图象都经过x轴上点A（4，0）和y轴上点B（0，﹣3），过动点M（m，0）（0＜m＜4）作x轴的垂线交直线AB于点C，交抛物线于点P．
1. （1）求b，c的值；
2. （2）点M在运动的过程中，能否使△PBC为直角三角形？如果能，求出点P的坐标；如果不能，请说明理由；
3. （3）如图2，过点P作PD⊥AB于点，设△PCD的面积为S₁ ， △ACM的面积为₂ ，若 $\text{[math]}$ = $\text{[math]}$ ，
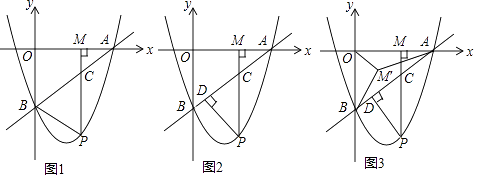
  ①求m的值；
  ②如图3，将线段OM绕点O顺时针旋转得到OM′，旋转角为α（0°＜α＜90°），连接M'A、M'B，求M'A+ $\text{[math]}$ M'B的最小值．
答案解析收藏纠错 + 选题