 B .
B .  C .
C .  D .
D . 

 B .
B . 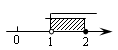 D .
D . 


|
考试成绩/分 |
30 |
29 |
28 |
27 |
26 |
|
学生数/人 |
20 |
15 |
10 |
2 |
2 |
该班中考英语听力口语模拟考试成绩的众数比中位数多分.

| 月均用水量(单位: | 频数 | 百分比 |
| | 2 | 4% |
| | 12 | 24% |
| |
|
|
| | 10 | 20% |
| |
| 12% |
| | 3 | 6% |
| | 2 | 4% |


①试求S关于t的函数关系式;
②在图2的直角坐标系中,画出S关于t的函数图象,并回答:S是否有最大值?若有,写出S的最大值;若没有,请说明理由.