浙江省宁波市镇海区2017-2018学年八年级下学期数学期末...

更新时间：2019-07-26 浏览次数：395 类型：期末考试

一、单选题

1. (2018八下·镇海期末) 要使二次根式 $\text{[math]}$ 有意义，则x的取值范围是（）

A . x<3 B . x≤3 C . x>3 D . x≥3

答案解析收藏纠错 + 选题
2. (2018八下·镇海期末) 下列图形中，既是轴对称图形又是中心对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
3. (2018八下·镇海期末) 百货商场试销一批新款衬衫，一周内销售情况如表所示，商场经理想要了解哪种型号最畅销，那么他最关注的统计量是（）

型号（厘米）

38

39

40

41

42

43

数量（件）

23

31

35

48

29

8

A . 平均数 B . 中位数 C . 众数 D . 方差

答案解析收藏纠错 + 选题
4. (2023九上·丰台期中) 用配方法解一元二次方程x²-8x+3=0，此方程可化为（）

A . (x-4)²=13 B . (x+4)²=13 C . (x-4)²=19 D . (x+4)²=19

答案解析收藏纠错 + 选题
5. (2021八上·蒙阴期中) 如图所示，小华从A点出发，沿直线前进10米后左转24°，再沿直线前进10米，又向左转24°，……，照这样走下去，他第一次回到出发地A点时，一共走的路程是（）

A . 140米 B . 150米 C . 160米 D . 240米

答案解析收藏纠错 + 选题
6. (2024八下·龙门期中) 下列说法中正确的是（）

A . 有一个角是直角的四边形是矩形 B . 两条对角线互相垂直的四边形是菱形 C . 两条对角线互相垂直平分的四边形是正方形 D . 两条对角线相等的菱形是正方形

答案解析收藏纠错 + 选题
7. (2021八下·余姚期中) 用反证法证明命题“在三角形中，至多有一个内角是直角”时，应先假设（）

A . 至少有一个内角是直角 B . 至少有两个内角是直角 C . 至多有一个内角是直角 D . 至多有两个内角是直角

答案解析收藏纠错 + 选题
8. (2018八下·镇海期末) 某楼盘2016年房价为每平方米15600元，经过两年连续降价后，2018年房价为每平方米12400元。设该楼盘这两年房价每年平均降低率为x，根据题意可列方程为（）

A . 15600(1-2x)=12400 B . 2×15600(1-2x)=12400 C . 15600(1-x)²=12400 D . 15600(1-x²)=12400

答案解析收藏纠错 + 选题
9. (2018八下·镇海期末) 如图，点A在双曲线 $\text{[math]}$ 上，点B在双曲线 $\text{[math]}$ 上，且AB∥y轴，C、D在y轴上，若四边形ABCD为矩形，则它的面积为（）

A . 1.5 B . 1 C . 3 D . 2

答案解析收藏纠错 + 选题
10. (2018八下·镇海期末) 二次函数y=ax²+bx+c(a≠0)的图象如图所示，下列结论：①a<0；②a-b+c<0；③b²-4ac>0；④2a+b＞0，其中正确的是（）

A . ①②③④ B . ②③④ C . ①②③ D . ①②④

答案解析收藏纠错 + 选题
11. (2022八下·浙江) 如图，在矩形纸片ABCD中，BC=a，将矩形纸片翻折，使点C恰好落在对角线交点O处，折痕为BE，点E在边CD上，则CE的长为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
12. (2022八下·金华月考) 一个大矩形按如图方式分割成6个小矩形，且只有标号为②，④的两个小矩形为正方形，若要求出△ABC的面积，则需要知道下列哪个条件？（）

A . ⑥的面积 B . ③的面积 C . ⑤的面积 D . ⑤的周长

答案解析收藏纠错 + 选题

二、填空题

13. (2020八下·南昌月考) $\text{[math]}$ 的计算结果是.

答案解析收藏纠错 + 选题
14. (2018八下·镇海期末) 有一组数据如下： $\text{[math]}$ 2， 2， 0，1， 4.那么这组数据的平均数为，方差为.

答案解析收藏纠错 + 选题
15. (2018八下·镇海期末) 如果关于x的方程 $\text{[math]}$ 有实数根，则m的取值范围是.

答案解析收藏纠错 + 选题
16. (2018八下·镇海期末) 如图，在平面直角坐标系中，直线y= $\text{[math]}$ 4x+4与x、y轴分别相交于点A、B，四边形ABCD是正方形，抛物线 $\text{[math]}$ 过C，D两点，且C为顶点，则a的值为.

答案解析收藏纠错 + 选题
17. (2018八下·镇海期末) 图，在正方向 $\text{[math]}$ 中， $\text{[math]}$ 是对角线 $\text{[math]}$ 上一点， $\text{[math]}$ 的延长线与FG 交于点 $\text{[math]}$ ，若 $\text{[math]}$ ，则 $\text{[math]}$ 。 1；

答案解析收藏纠错 + 选题
18. (2018八下·镇海期末) 如图，四边形ABCD为菱形，点A在y轴正半轴上，AB∥x轴，点B，C在反比例函数 $\text{[math]}$ 上，点D在反比例函数 $\text{[math]}$ 上，那么点D的坐标为.

答案解析收藏纠错 + 选题

三、解答题

19. (2018八下·镇海期末) 计算： $\text{[math]}$

答案解析收藏纠错 + 选题
20. (2023八下·淮北期末) 解方程：
1. （1） $\text{[math]}$
2. （2） $\text{[math]}$
答案解析收藏纠错 + 选题
21. (2018八下·镇海期末) 为了解初二学生参加户外活动的情况，某县教育局对其中500名初二学生每天参加户外活动的时间进行抽样调查，并将调查结果绘制成如下统计图。（参加户外活动的时间分为四种类别：“0.5小时”，“1小时”，“1.5小时”，“2小时”）

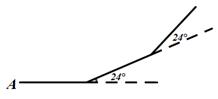
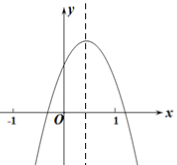
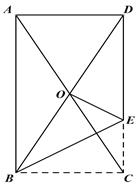
请根据图示，回答下列问题：
1. （1）求学生每天户外活动时间的平均数，众数和中位数；
2. （2）该县共有12000名初二学生，请估计该县每天户外活动时间超过1小时的初二学生有多少人?
答案解析收藏纠错 + 选题
22. (2018八下·镇海期末) 如图，在平面直角坐标系中，直线y₁=x+1与双曲线 $\text{[math]}$ （k＞0）相交于点A、B，已知点A坐标（2，m）.
1. （1）求k的值；
2. （2）求点B的坐标，并观察图象，写出当 $\text{[math]}$ 时，x的取值范围.
答案解析收藏纠错 + 选题
23. (2021八下·北仑期中) 百货商店销售某种冰箱，每台进价2500元.市场调研表明：当销售价为2900元时，平均每天能售出8台；每台售价每降低10元时，平均每天能多售出1台.（销售利润=销售价-进价）
1. （1）如果设每台冰箱降价x元，那么每台冰箱的销售利润为元，平均每天可销售冰箱台；（用含x的代数式表示）
2. （2）商店想要使这种冰箱的销售利润平均每天达到5600元，且尽可能地清空冰箱库存，每台冰箱的定价应为多少元？
答案解析收藏纠错 + 选题
24. (2018八下·镇海期末) 如图，在矩形ABCD中，AB=4，AD=10，点E在AD边上，已知B、E两点关于直线l对称，直线l分别交AD、BC边于点M、N，连接BM、NE.
1. （1）求证：四边形BMEN是菱形；
2. （2）若DE=2，求NC的长.
答案解析收藏纠错 + 选题
25. (2019九上·合肥月考) 如图，抛物线y=﹣x²+bx+c（a≠0）与x轴交于点A（﹣1，0）和B（3，0），与y轴交于点C，点D的横坐标为m（0＜m＜3），连结DC并延长至E，使得CE=CD，连结BE，BC.
1. （1）求抛物线的解析式；
2. （2）用含m的代数式表示点E的坐标，并求出点E纵坐标的范围；
3. （3）求△BCE的面积最大值.
答案解析收藏纠错 + 选题
26. (2018八下·镇海期末) 如图，四边形OABC为矩形，点B坐标为（4，2），A，C分别在x轴，y轴上，点F在第一象限内，OF的长度不变，且反比例函数 $\text{[math]}$ 经过点F.
1. （1）如图1，当F在直线y = x上时，函数图象过点B，求线段OF的长.
2. （2）如图2，若OF从（1）中位置绕点O逆时针旋转，反比例函数图象与BC，AB相交，交点分别为D，E，连结OD，DE，OE.
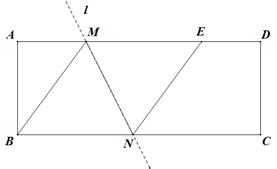
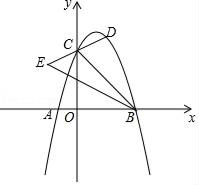
  ①求证：CD=2AE.
  
  ②若AE+CD=DE，求k.
  
  ③设点F的坐标为（a，b），当△ODE为等腰三角形时，求（a+b）²的值.
答案解析收藏纠错 + 选题