广东省惠州市龙门县2023-2024学年八年级下学期数学期中...

更新时间：2024-06-24 浏览次数：55 类型：期中考试

一、选择题（本大题3小题，每小题3分，共30分）

1. (2024八下·龙门期中) 使式子 $\text{[math]}$ 有意义的x的取值范围是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2024九下·武威模拟) 下列计算正确的是（　　）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2024九上·衡阳月考) 下列各式中，能与 $\text{[math]}$ 合并的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2024八下·南充期中) 以下列各组数为边长，能组成直角三角形的是（）

A . 3，4，5 B . 2，3，4 C . 4，5，6 D . 8，9，10

答案解析收藏纠错 + 选题
5. (2024八下·龙门期中) 下列说法中正确的是（）

A . 有一个角是直角的四边形是矩形 B . 两条对角线互相垂直的四边形是菱形 C . 两条对角线互相垂直平分的四边形是正方形 D . 两条对角线相等的菱形是正方形

答案解析收藏纠错 + 选题
6. (2024八下·龙门期中) 如图，平地上A、B两点被池塘隔开，测量员在岸边选一点C，并分别找到AC和BC的中点D、E，测量得DE=16米，则A、B两点间的距离为（）

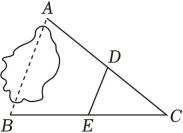
A . 30米 B . 32米 C . 36米 D . 48米

答案解析收藏纠错 + 选题
7. (2024八下·龙门期中) 如图，在四边形 $\text{[math]}$ 中，对角线 $\text{[math]}$ 与 $\text{[math]}$ 相交于点 $\text{[math]}$ ，下列条件不能判定四边形 $\text{[math]}$ 是平行四边形的是（）

A . $\text{[math]}$ ， $\text{[math]}$ B . $\text{[math]}$ ， $\text{[math]}$ C . $\text{[math]}$ ， $\text{[math]}$ D . $\text{[math]}$ ， $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2024八上·柯桥月考) 在勾股定理的学习过程中，我们已经学会了运用如下图形，验证著名的勾股定理，这种根据图形直观推论或验证数学规律和公式的方法，简称为“无字证明”，实际上它也可用于验证数与代数、图形与几何等领域中的许多数学公式和规律，它体现的数学思想是（）

A . 统计思想 B . 分类思想 C . 数形结合思想 D . 方程思想

答案解析收藏纠错 + 选题
9. (2024八下·龙门期中) 如图，将长方形 $\text{[math]}$ 沿对角线 $\text{[math]}$ 对折，使点 $\text{[math]}$ 落在点 $\text{[math]}$ 处， $\text{[math]}$ 交 $\text{[math]}$ 于 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则重叠部分（即 $\text{[math]}$ ）的面积为（）

A . 24 B . 30 C . 40 D . 80

答案解析收藏纠错 + 选题
10. (2024八下·龙门期中) 如图，已知菱形 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 为 $\text{[math]}$ 的中点， $\text{[math]}$ 为对角线 $\text{[math]}$ 上一点，则 $\text{[math]}$ 的最小值等于（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . 8

答案解析收藏纠错 + 选题

二、填空题（本大题共5小题，每小题3分，共15分）

11. (2024八下·龙门期中) 比较大小： $\text{[math]}$ $\text{[math]}$ ．（填“ $\text{[math]}$ ”“ $\text{[math]}$ ”或“ $\text{[math]}$ ”）

答案解析收藏纠错 + 选题
12. (2024八下·龙门期中) 化简 $\text{[math]}$ 的结果为．

答案解析收藏纠错 + 选题
13. (2024八下·龙门期中) 已知一个直角三角形的两边长分别为6和8，则另一条边长为．

答案解析收藏纠错 + 选题
14. (2024八下·龙门期中) 如图，在平行四边形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 于 $\text{[math]}$ ，则 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
15. (2024八下·龙门期中) 如图， $\text{[math]}$ 是矩形 $\text{[math]}$ 的对角线 $\text{[math]}$ 上一点，过点 $\text{[math]}$ 作 $\text{[math]}$ ，分别交 $\text{[math]}$ ， $\text{[math]}$ 于点 $\text{[math]}$ ， $\text{[math]}$ ，连接 $\text{[math]}$ ， $\text{[math]}$ ．若 $\text{[math]}$ ， $\text{[math]}$ ，则图中阴影部分的面积为．

答案解析收藏纠错 + 选题

三、解答题（一）（16题10分，每小题5分，17、18题各7分，共24分）

16. (2024八下·龙门期中)
1. （1） $\text{[math]}$
2. （2） $\text{[math]}$
答案解析收藏纠错 + 选题
17. (2024八下·龙门期中) 已知：如图，四边形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，求四边形 $\text{[math]}$ 的面积．

答案解析收藏纠错 + 选题
18. (2024八下·龙门期中) 如图，在平行四边形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ 是对角线 $\text{[math]}$ 上的两点，且 $\text{[math]}$ ，求证： $\text{[math]}$ ．

答案解析收藏纠错 + 选题

四、解答题（二）（本大题共3小题，每小题9分，共27分）

19. (2024八下·龙门期中) 阅读理解题，下面我们观察：
$\text{[math]}$ ．反之 $\text{[math]}$ ，所以 $\text{[math]}$ ，所以 $\text{[math]}$ ．
完成下列各题：
1. （1）把 $\text{[math]}$ 写成 $\text{[math]}$ 的形式；
2. （2）化简： $\text{[math]}$ ；
3. （3）化简： $\text{[math]}$ ．
答案解析收藏纠错 + 选题
20. (2024八下·龙门期中) 如图，平行四边形 $\text{[math]}$ 中， $\text{[math]}$ ，过点 $\text{[math]}$ 作 $\text{[math]}$ 交 $\text{[math]}$ 的延长线于点 $\text{[math]}$ ，点 $\text{[math]}$ 为 $\text{[math]}$ 的中点，连接 $\text{[math]}$ ．
1. （1）求证：四边形 $\text{[math]}$ 是矩形；
2. （2）若 $\text{[math]}$ ，且 $\text{[math]}$ ，求四边形 $\text{[math]}$ 的面积．
答案解析收藏纠错 + 选题
21. (2024八下·龙门期中) “为了安全，请勿超速”．如图，一条公路建成通车，在迎宾大道 $\text{[math]}$ 上限速60千米/小时，为了检测车辆是否超速，在公路 $\text{[math]}$ 旁设立了观测点 $\text{[math]}$ ，从观测点 $\text{[math]}$ 测得一小车从点 $\text{[math]}$ 到达点 $\text{[math]}$ 行驶了5秒，已知 $\text{[math]}$ ， $\text{[math]}$ 米， $\text{[math]}$ 米．
1. （1）请求出观测点 $\text{[math]}$ 到公路 $\text{[math]}$ 的距离：
2. （2）此车超速了吗？请说明理由．（参考数据： $\text{[math]}$ ， $\text{[math]}$ ）
答案解析收藏纠错 + 选题

五、解答题（三）（本大题共2小题，每小题12分，共24分）

22. (2024八下·龙门期中) 综合与实践课上，老师带领同学们以“矩形和平行四边形的折叠”为主题开展数学活动．
1. （1）操作判断：
  如图1，在矩形 $\text{[math]}$ 中，点 $\text{[math]}$ 为边 $\text{[math]}$ 的中点，沿 $\text{[math]}$ 折叠，使点 $\text{[math]}$ 落在点 $\text{[math]}$ 处，把纸片展平，延长 $\text{[math]}$ 与 $\text{[math]}$ 交于点 $\text{[math]}$ ．请写出线段 $\text{[math]}$ 与线段 $\text{[math]}$ 的数量关系，并说明理由.
2. （2）迁移思考：
  如图1，若 $\text{[math]}$ ，按照（1）中的操作进行折叠和作图，当 $\text{[math]}$ 时，求 $\text{[math]}$ 的值.
3. （3）拓展探索：
  如图2，四边形 $\text{[math]}$ 为平行四边形，其中 $\text{[math]}$ 与 $\text{[math]}$ 是对角，点 $\text{[math]}$ 为边 $\text{[math]}$ 的中点，沿 $\text{[math]}$ 折叠，使点 $\text{[math]}$ 落在点 $\text{[math]}$ 处，把纸片展平，延长 $\text{[math]}$ 与射线 $\text{[math]}$ 交于点 $\text{[math]}$ ．若 $\text{[math]}$ ， $\text{[math]}$ ，请直接写出线段 $\text{[math]}$ 的值．
答案解析收藏纠错 + 选题
23. (2024八下·龙门期中) 已知，如图， $\text{[math]}$ 为坐标原点，四边形 $\text{[math]}$ 为矩形， $\text{[math]}$ ， $\text{[math]}$ ，点 $\text{[math]}$ 是 $\text{[math]}$ 的中点，动点 $\text{[math]}$ 在线段 $\text{[math]}$ 上以每秒2个单位长的速度由点 $\text{[math]}$ 向 $\text{[math]}$ 运动．设动点 $\text{[math]}$ 的运动时间为 $\text{[math]}$ 秒．
1. （1）当 $\text{[math]}$ 为何值时，四边形 $\text{[math]}$ 是平行四边形；
2. （2）在直线 $\text{[math]}$ 上是否存在一点 $\text{[math]}$ ，使得 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 四点为顶点的四边形是菱形？若存在，求 $\text{[math]}$ 的值，并求出 $\text{[math]}$ 点的坐标；若不存在，请说明理由．
3. （3）在线段 $\text{[math]}$ 上有一点 $\text{[math]}$ 且 $\text{[math]}$ ，直接写出四边形 $\text{[math]}$ 的周长的最小值，并在图上画图标出点 $\text{[math]}$ 的位置．
答案解析收藏纠错 + 选题