广东省深圳市2019年高一下学期数学期末考试试卷

更新时间：2024-07-13 浏览次数：733 类型：期末考试

一、选择题:本大题共10小题，每小题5分，共50分。

1. (2019高一下·深圳期末) 若集合A={-2，1，2，3}，B={x|x=2n，n∈N}，则A∩B=（）

A . {-2} B . {2} C . {-2，2} D . ∅

答案解析收藏纠错 + 选题
2. 连续两次抛掷一枚质地均匀的硬币，出现正面向上与反面向上各一次的概率是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2019高一下·深圳期末) 下列函数中，既是偶函数又在区间(0，+∞)上单调递减的是（）

A . y=x³ B . y=|x| C . y=sinx D . y= $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2019高一下·深圳期末) 如图，扇形OAB的圆心角为90°，半径为1，则该扇形绕OB所在直线旋转一周得到的几何体的表面积为（）

A . $\text{[math]}$ B . 2π C . 3π D . 4π

答案解析收藏纠错 + 选题
5. (2019高一下·深圳期末) 已知函数f(x)=cosx，下列结论不正确的是（）

A . 函数y=f(x)的最小正周期为2π B . 函数y=f(x)在区间(0，π)内单调递减 C . 函数y=f(x)的图象关于y轴对称 D . 把函数y=f(x)的图象向左平移 $\text{[math]}$ 个单位长度可得到y=sinx的图象

答案解析收藏纠错 + 选题
6. (2019高一下·深圳期末) 已知直线l是平面a的斜线，则a内不存在与l（）

A . 相交的直线 B . 平行的直线 C . 异面的直线 D . 垂直的直线

答案解析收藏纠错 + 选题
7. (2019高一下·深圳期末) 若a>0，且a≠1，则“a= $\text{[math]}$ ”是“函数f(x)=log_ax-x有零点”的（）

A . 充分不必要条件 B . 必要不充分条件 C . 充要条件 D . 既不充分也不必要条件

答案解析收藏纠错 + 选题
8. (2019高一下·深圳期末) 如图，△ABC中，E，F分别是BC，AC边的中点，AE与BF相交于点G，则 $\text{[math]}$ =（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2019高一下·深圳期末) 英国数学家布鲁克泰勒( Taylor Brook，1685~1731)建立了如下正、余弦公式（）
sinx=x- $\text{[math]}$

cosx-1= $\text{[math]}$

其中x∈R，n∈N*，n!=1×2×3×4x…xn，例如：1!=1，2!=2，3!=6。试用上述公式估计cos0.2的近似值为(精确到0.01)

A . 0.99 B . 0.98 C . 0.97 D . 0.96

答案解析收藏纠错 + 选题
10. (2019高一下·深圳期末) 已知函数f(x)=m·2^x+x+m²-2，若存在实数x，满足f(-x)=-f(x)，则实数m的取值范围为（）

A . (-∞，-2]U(0，1] B . [-2，0)U(0，1] C . [-2，0)U[1，+∞) D . (-∞，-2]U[1，+∞)

答案解析收藏纠错 + 选题

二、填空题:本大题共6小题，共32分，其中第11-14题，每小题5分，第15、16小题，每小题都有两个空、每个空3分．

11. (2019高一下·深圳期末) 设i为虚数单位，复数z=i(4+3i)的模为。

答案解析收藏纠错 + 选题
12. (2019高一下·深圳期末) 已知 $\text{[math]}$ =(2，4)， $\text{[math]}$ =(1，3)，则 $\text{[math]}$ =．

答案解析收藏纠错 + 选题
13. (2019高一下·深圳期末) 甲、乙两名射击运动员进行射击比赛，甲的中靶概率为0.8，乙的中靶概率为0.7，现两人各自独立射击一次，均中靶的概率为．

答案解析收藏纠错 + 选题
14. (2020高一下·佛山月考) 某学校高一年级举行选课培训活动，共有1024名学生、家长、老师参加，其中家长256人．学校按学生、家长、老师分层抽样，从中抽取64人，进行某问卷调查，则抽到的家长有人

答案解析收藏纠错 + 选题
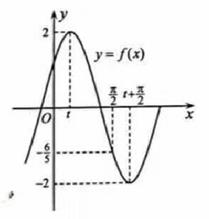
15. (2019高一下·深圳期末) 函数f(x)=Asin( $\text{[math]}$ x+ $\text{[math]}$ )的部分图象如图，其中A>0， $\text{[math]}$ >0，0< $\text{[math]}$ < $\text{[math]}$ ．则 $\text{[math]}$ = ； tan $\text{[math]}$ = ．

答案解析收藏纠错 + 选题
16. (2019高一下·深圳期末) 棱长均为1m的正三棱柱透明封闭容器盛有am³水，当侧面AA₁B₁B水平放置时，液面高为hm(如图1)；当转动容器至截面A₁BC水平放置时，盛水恰好充满三棱锥A-A₁BC(如图2)，则a= ；h= ．

答案解析收藏纠错 + 选题

三、解答题:本大题共5小题，第17题12分，其余每小题14分，共68分．

17. (2019高一下·深圳期末) 已知△BC的三个内角A，B，C的对边分别是a，b，c，a>c，且2csinA= $\text{[math]}$ a．
1. （1）求角C的大小;
2. （2）若c=4，△ABC的面积为 $\text{[math]}$ ，求△ABC的周长
答案解析收藏纠错 + 选题
18. (2019高一下·深圳期末) 如图，在平面直角坐标系xOy中，点A为单位圆与x轴正半轴的交点，点P为单位圆上的一点，且∠AOP= $\text{[math]}$ ，点P沿单位圆按逆时针方向旋转角θ后到点Q(a，b)
1. （1）当θ= $\text{[math]}$ 时，求ab的值
2. （2）设θ∈[ $\text{[math]}$ ， $\text{[math]}$ ]，求b-a的取值范围
答案解析收藏纠错 + 选题

19. (2019高一下·深圳期末) 某科研课题组通过一款手机APP软件，调查了某市1000名跑步爱好者平均每周的跑步量(简称“周跑量”)，得到如下的频数分布表

周跑量(km/周)	[10，15 )	[15，20 )	[20，25 )	[25，30 )	[30，35 )	[35，40 )	[40，45 )	[45，50 )	[50，55 )
人数	100	120	130	180	220	150	60	30	10

（1）在答题卡上补全该市1000名跑步爱好者周跑量的频率分布直方图：

注：请先用铅笔画，确定后再用黑色水笔描黑
（2）根据以上图表数据计算得样本的平均数为28.5km，试求样本的中位数(保留一位小数)，并用平均数、中位数等数字特征估计该市跑步爱好者周跑量的分布特点

（3）根据跑步爱好者的周跑量，将跑步爱好者分成以下三类，不同类别的跑者购买的装备的价格不一样，如下表：

周跑量	小于20公里	20公里到40公里	不小于40公里
类别	休闲跑者	核心跑者	精英跑者
装备价格（单位：元）	2500	4000	4500

根据以上数据，估计该市每位跑步爱好者购买装备，平均需要花费多少元?

答案解析收藏纠错 + 选题

20. (2019高一下·深圳期末) 如图长方体ABCD-A₁B₁C₁D₁中，AB= $\text{[math]}$ AD，E，F分别为棱AB，A₁D₁的中点
1. （1）求证：平面EFC⊥平面BB₁D；
2. （2）请在答题卡图形中画出直线DB₁与平面EFC的交点O(保留必要的辅助线)，写出画法并计算 $\text{[math]}$ 的值(不必写出计算过程)
答案解析收藏纠错 + 选题
21. (2019高一下·深圳期末) 已知函数f(x)= $\text{[math]}$ ，其中a∈R．
1. （1）当a=1时，求f(x)的最小值;
2. （2）设函数f(x)恰有两个零点x₁ ， x₂ ，且x₂-x₁>2，求a的取值范围
答案解析收藏纠错 + 选题

试卷信息

小学

初中

高中

广东省深圳市2019年高一下学期数学期末考试试卷

副标题：

*注意事项：

广东省深圳市2019年高一下学期数学期末考试试卷

试题分析

总体分析

题量分析

难度分析

知识点分析